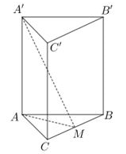
Câu hỏi: Cho lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh $2a.$ Gọi $M$ là trung điểm của $BC,$ biết góc giữa đường thẳng $A'M$ và mặt phẳng $\left( ABC \right)$ bằng ${{60}^{0}}$ (tham khảo hình bên). Khoảng cách từ điểm $A'$ đến mặt phẳng $\left( ABC \right)$ bằng
A. $\sqrt{3}a.$
B. $2a.$
C. $a.$
D. $3a.$

A. $\sqrt{3}a.$
B. $2a.$
C. $a.$
D. $3a.$
Ta có $AM=\sqrt{A{{C}^{2}}-C{{M}^{2}}}=\sqrt{3}a,$ góc giữa đường thẳng $A'M$ và mặt phẳng $\left( ABC \right)$ là $\widehat{A'MA}={{60}^{0}}.$ Khi đó $\tan \widehat{A'MA}=\tan {{60}^{0}}=\dfrac{A'A}{AM}\Rightarrow A'A=AM.\tan {{60}^{0}}=3a.$
Vậy khoảng cách từ điểm $A'$ đến mặt phẳng $\left( ABC \right)$ bằng $3a.$
Vậy khoảng cách từ điểm $A'$ đến mặt phẳng $\left( ABC \right)$ bằng $3a.$
Đáp án D.