Google
Câu hỏi: Cho lăng trụ $ABC.A'B'C'$ có đáy là tam giác đều cạnh $a$, hình chiếu vuông góc của $A$ lên $\left( ABC \right)$ trùng với trọng tâm của tam giác $ABC$. Một mặt phẳng $\left( P \right)$ chứa $BC$ và vuông góc với $AA'$ cắt hình lăng trụ $ABC.A'B'C'$ theo một thiết diện có diện tích bằng $\dfrac{{{a}^{2}}\sqrt{3}}{8}$. Thể tích khối lăng trụ đã cho bằng
A. $\dfrac{{{a}^{3}}\sqrt{3}}{4}$.
B. $\dfrac{2{{a}^{3}}\sqrt{3}}{3}$.
C. $\dfrac{{{a}^{3}}\sqrt{3}}{12}$.
D. $\dfrac{{{a}^{3}}\sqrt{3}}{10}$.
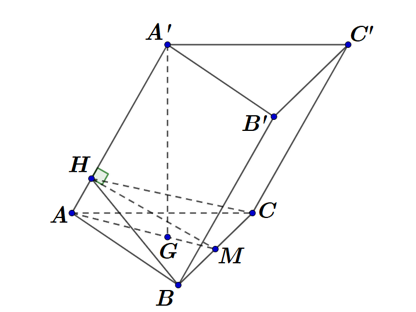Gọi $M$ là trung điểm $BC$ $\Rightarrow $ $\left( AA'M \right)$ là mặt phẳng trung trực của $BC$ $\Rightarrow BC\bot \left( AA'M \right)$.
Kẻ $MH\bot AA'$ $\Rightarrow AA'\bot \left( HBC \right)\Rightarrow \left( HBC \right)\equiv \left( P \right)$.
Khi đó thiết diện tạo bởi $\left( P \right)$ và lăng trụ $ABC.A'B'C'$ là tam giác $HBC$.
Ta có ${{S}_{HBC}}=\dfrac{1}{2}HM.BC=\dfrac{{{a}^{2}}\sqrt{3}}{8}\Leftrightarrow HM=\dfrac{a\sqrt{3}}{4}$ $\Rightarrow d\left( G,AA' \right)=\dfrac{2}{3}d\left( M,AA' \right)=\dfrac{2}{3}HM=\dfrac{a\sqrt{3}}{6}$.
Xét tam giác $A'GA$ vuông tại $G$, ta có:
$\dfrac{1}{{{d}^{2}}\left( G,AA' \right)}=\dfrac{1}{G{{A}^{2}}}+\dfrac{1}{GA{{'}^{2}}}\Leftrightarrow \dfrac{1}{{{\left( \dfrac{a\sqrt{3}}{6} \right)}^{2}}}=\dfrac{1}{{{\left( \dfrac{a\sqrt{3}}{2}.\dfrac{2}{3} \right)}^{2}}}+\dfrac{1}{GA{{'}^{2}}}\Leftrightarrow GA'=\dfrac{1}{3}\Rightarrow {{V}_{ABC.A'B'C'}}=\dfrac{{{a}^{2}}\sqrt{3}}{12}$.
B. $\dfrac{2{{a}^{3}}\sqrt{3}}{3}$.
C. $\dfrac{{{a}^{3}}\sqrt{3}}{12}$.
D. $\dfrac{{{a}^{3}}\sqrt{3}}{10}$.
Kẻ $MH\bot AA'$ $\Rightarrow AA'\bot \left( HBC \right)\Rightarrow \left( HBC \right)\equiv \left( P \right)$.
Khi đó thiết diện tạo bởi $\left( P \right)$ và lăng trụ $ABC.A'B'C'$ là tam giác $HBC$.
Ta có ${{S}_{HBC}}=\dfrac{1}{2}HM.BC=\dfrac{{{a}^{2}}\sqrt{3}}{8}\Leftrightarrow HM=\dfrac{a\sqrt{3}}{4}$ $\Rightarrow d\left( G,AA' \right)=\dfrac{2}{3}d\left( M,AA' \right)=\dfrac{2}{3}HM=\dfrac{a\sqrt{3}}{6}$.
Xét tam giác $A'GA$ vuông tại $G$, ta có:
$\dfrac{1}{{{d}^{2}}\left( G,AA' \right)}=\dfrac{1}{G{{A}^{2}}}+\dfrac{1}{GA{{'}^{2}}}\Leftrightarrow \dfrac{1}{{{\left( \dfrac{a\sqrt{3}}{6} \right)}^{2}}}=\dfrac{1}{{{\left( \dfrac{a\sqrt{3}}{2}.\dfrac{2}{3} \right)}^{2}}}+\dfrac{1}{GA{{'}^{2}}}\Leftrightarrow GA'=\dfrac{1}{3}\Rightarrow {{V}_{ABC.A'B'C'}}=\dfrac{{{a}^{2}}\sqrt{3}}{12}$.
Đáp án C.