Câu hỏi: Cho khối lăng trụ đứng
A.
B.
C.
D.
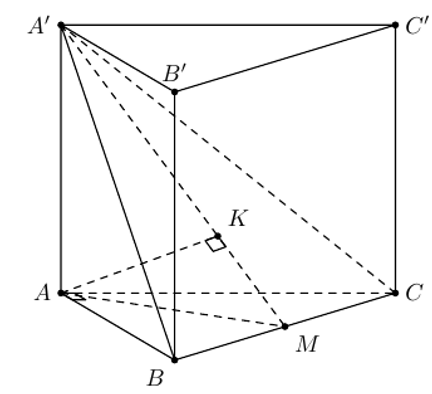 Gọi
Gọi
Khi đó
Trong
Khi đó
Trong
Ta có
Vậy thể tích của khối lăng trụ
A.
B.
C.
D.
Khi đó
Trong
Khi đó
Trong
Ta có
Vậy thể tích của khối lăng trụ
Đáp án D.