Google
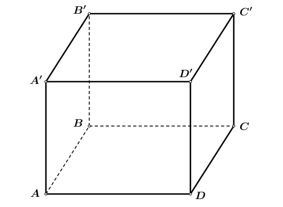
Câu hỏi: Cho khối hộp chữ nhật $ABCD.{A}'{B}'{C}'{D}'$ có $AB=a,AD=2a,$ diện tích tam giác ${C}'BD$ bằng $\sqrt{6}{{a}^{2}}$ (tham khảo hình vẽ)
Thể tích của khối hộp chữ nhật đã cho bằng
A. $4{{a}^{3}}$.
B. $2\sqrt{6}{{a}^{3}}$.
C. $\dfrac{2\sqrt{6}}{3}{{a}^{3}}$.
D. $\dfrac{4}{3}{{a}^{3}}$.
Trong mp $\left( ABCD \right),$ kẻ $CH\bot BD$ thì $BD\bot \left( CH{C}' \right)\Rightarrow BD\bot H{C}'$.
Khi đó
$\Delta CBD$ vuông tại $C$ có $BD=\sqrt{B{{C}^{2}}+C{{D}^{2}}}=a\sqrt{5}$ và $CH=\dfrac{BC.CD}{\sqrt{B{{C}^{2}}+C{{D}^{2}}}}=\dfrac{2a}{\sqrt{5}}$.
${{S}_{{C}'BD}}=\dfrac{1}{2}H{C}'.BD\Leftrightarrow H{C}'=\dfrac{2{{S}_{{C}'BD}}}{BD}=\dfrac{2\sqrt{6}a}{\sqrt{5}}$.
Tam giác $HC{C}'$ vuông tại $C$ có $C{C}'=\sqrt{H{{{{C}'}}^{2}}-H{{C}^{2}}}=2a.$
Vậy thể tích khối hôph chữ nhật đã cho là $V={{S}_{ABCD}}.C{C}'=4{{a}^{3}}$.
A. $4{{a}^{3}}$.
B. $2\sqrt{6}{{a}^{3}}$.
C. $\dfrac{2\sqrt{6}}{3}{{a}^{3}}$.
D. $\dfrac{4}{3}{{a}^{3}}$.
Khi đó
$\Delta CBD$ vuông tại $C$ có $BD=\sqrt{B{{C}^{2}}+C{{D}^{2}}}=a\sqrt{5}$ và $CH=\dfrac{BC.CD}{\sqrt{B{{C}^{2}}+C{{D}^{2}}}}=\dfrac{2a}{\sqrt{5}}$.
${{S}_{{C}'BD}}=\dfrac{1}{2}H{C}'.BD\Leftrightarrow H{C}'=\dfrac{2{{S}_{{C}'BD}}}{BD}=\dfrac{2\sqrt{6}a}{\sqrt{5}}$.
Tam giác $HC{C}'$ vuông tại $C$ có $C{C}'=\sqrt{H{{{{C}'}}^{2}}-H{{C}^{2}}}=2a.$
Vậy thể tích khối hôph chữ nhật đã cho là $V={{S}_{ABCD}}.C{C}'=4{{a}^{3}}$.
Đáp án A.