Google
Câu hỏi: Cho hình trụ có thiết diện qua trục là một hình vuông. Gọi ${{S}_{1}},{{S}_{2}}$ lần lượt là diện tích xung quanh và diện tích toàn phần của hình trụ đã cho. Tỷ số $\dfrac{{{S}_{1}}}{{{S}_{2}}}$ bằng
A. $\dfrac{2}{3}$.
B. $\dfrac{1}{2}$.
C. $\dfrac{4}{5}$.
D. $\dfrac{3}{4}$.
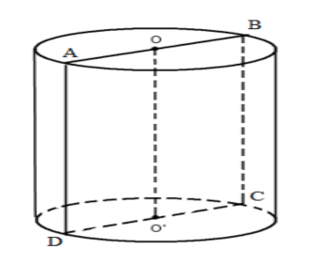Gọi thiết diện qua trục là hình vuông $ABCD$ có cạnh là $a$ suy ra $r=\dfrac{a}{2};l=a$
Ta có $\dfrac{{{S}_{1}}}{{{S}_{2}}}=\dfrac{2\pi rl}{2\pi rl+2\pi {{r}^{2}}}=\dfrac{\pi {{a}^{2}}}{\pi {{a}^{2}}+\pi \dfrac{{{a}^{2}}}{2}}=\dfrac{2}{3}$.
A. $\dfrac{2}{3}$.
B. $\dfrac{1}{2}$.
C. $\dfrac{4}{5}$.
D. $\dfrac{3}{4}$.
Ta có $\dfrac{{{S}_{1}}}{{{S}_{2}}}=\dfrac{2\pi rl}{2\pi rl+2\pi {{r}^{2}}}=\dfrac{\pi {{a}^{2}}}{\pi {{a}^{2}}+\pi \dfrac{{{a}^{2}}}{2}}=\dfrac{2}{3}$.
Đáp án A.