Google
Câu hỏi: Cho hình trụ có diện tích toàn phần bằng $9\pi $ và có thiết diện cắt bởi mặt phẳng qua trục là một hình vuông. Thể tích khối trụ đã cho là
A. $3\pi \sqrt{6}$.
B. $\dfrac{3\pi \sqrt{6}}{2}$.
C. $\dfrac{3\pi \sqrt{6}}{4}$.
D. $\dfrac{2\pi \sqrt{6}}{3}$.
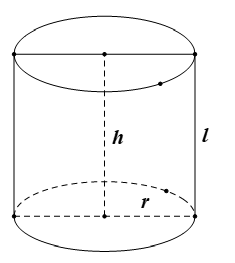Gọi $r$ là bán kính đáy của hình trụ.
Vì hình trụ có thiết diện cắt bởi mặt phẳng qua trục là một hình vuông nên hình trụ đó có chiều cao $h=l=2r$.
Diện tích toàn phần của hình trụ là ${{S}_{tp}}=2\pi {{r}^{2}}+2\pi rl=2\pi {{r}^{2}}+4\pi {{r}^{2}}=6\pi {{r}^{2}}$.
Theo bài ra, ta có $6\pi {{r}^{2}}=9\pi \Leftrightarrow r=\dfrac{\sqrt{6}}{2}$.
Do đó thể tích khối trụ là $V=\pi {{r}^{2}}h=2\pi {{r}^{3}}=2\pi {{\left( \dfrac{\sqrt{6}}{2} \right)}^{3}}=\dfrac{3\pi \sqrt{6}}{2}$.
A. $3\pi \sqrt{6}$.
B. $\dfrac{3\pi \sqrt{6}}{2}$.
C. $\dfrac{3\pi \sqrt{6}}{4}$.
D. $\dfrac{2\pi \sqrt{6}}{3}$.
Vì hình trụ có thiết diện cắt bởi mặt phẳng qua trục là một hình vuông nên hình trụ đó có chiều cao $h=l=2r$.
Diện tích toàn phần của hình trụ là ${{S}_{tp}}=2\pi {{r}^{2}}+2\pi rl=2\pi {{r}^{2}}+4\pi {{r}^{2}}=6\pi {{r}^{2}}$.
Theo bài ra, ta có $6\pi {{r}^{2}}=9\pi \Leftrightarrow r=\dfrac{\sqrt{6}}{2}$.
Do đó thể tích khối trụ là $V=\pi {{r}^{2}}h=2\pi {{r}^{3}}=2\pi {{\left( \dfrac{\sqrt{6}}{2} \right)}^{3}}=\dfrac{3\pi \sqrt{6}}{2}$.
Đáp án B.