Google
Câu hỏi: Cho hình trụ có bán kinh đáy bằng $\sqrt{3} a$. Cắt hình trụ bởi một mặt phằng song song với trục, cách trục một khoảng bằng $\sqrt{2} a$ ta được thiết diện là một hình chữ nhật có chu vi bằng $10a$. Thể tích khối trụ đã cho bằng
A. $27 \pi a^3$.
B. $3 \pi a^3$.
C. $9 \pi a^3$.
D. $12 \pi a^3$.
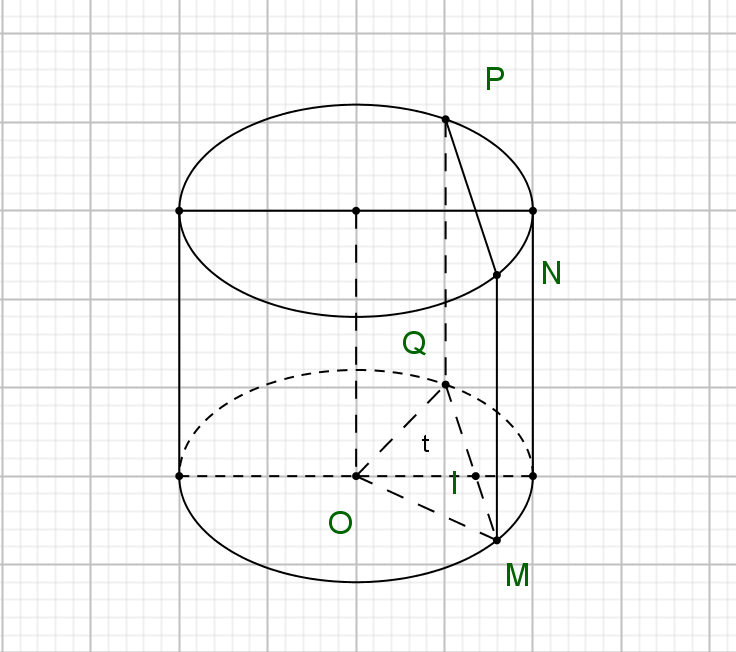Gọi thiết diện là $MNPQ$. Gọi $I$ là trung điểm của $MQ$. Ta có $MNPQ$ là hình chữ nhật.
Ta có $d\left( O,\left( MNPQ \right) \right)=OI=a\sqrt{2}$.
Tam giác $MIO$ vuông tại $O\Rightarrow MI=\sqrt{O{{M}^{2}}-O{{I}^{2}}}=\sqrt{{{\left( a\sqrt{3} \right)}^{2}}-{{\left( a\sqrt{2} \right)}^{^{2}}}}=a\Rightarrow MQ=2a.$
Do $MNPQ$ là hình chũ nhật nên $2\left( MN+MQ \right)=10a\Rightarrow MN=3a.$
Gọi $V$ là thể tích khối trụ, ta có $V=\pi {{r}^{2}}MN=\pi .3{{a}^{2}}.3a=9\pi {{a}^{3}}.$
A. $27 \pi a^3$.
B. $3 \pi a^3$.
C. $9 \pi a^3$.
D. $12 \pi a^3$.
Ta có $d\left( O,\left( MNPQ \right) \right)=OI=a\sqrt{2}$.
Tam giác $MIO$ vuông tại $O\Rightarrow MI=\sqrt{O{{M}^{2}}-O{{I}^{2}}}=\sqrt{{{\left( a\sqrt{3} \right)}^{2}}-{{\left( a\sqrt{2} \right)}^{^{2}}}}=a\Rightarrow MQ=2a.$
Do $MNPQ$ là hình chũ nhật nên $2\left( MN+MQ \right)=10a\Rightarrow MN=3a.$
Gọi $V$ là thể tích khối trụ, ta có $V=\pi {{r}^{2}}MN=\pi .3{{a}^{2}}.3a=9\pi {{a}^{3}}.$
Đáp án C.