Google
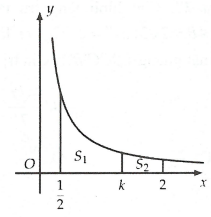
Câu hỏi: Cho hình thang cong (H) giới hạn bởi các đường $y=\dfrac{1}{x}, x=\dfrac{1}{2}, x=2$ và trục hoành. Đường thẳng $x=k \left( \dfrac{1}{2}<k<2 \right)$ chia hình (H) thành hai phần có diện tích ${{S}_{1}}$ và ${{S}_{2}}$ như hình vẽ.
Tất cả các giá trị thực của k để ${{S}_{1}}=3{{S}_{2}}$ thuộc khoảng nào dưới đây?
A. $\left( 1; 2 \right)$
B. $\left( 2; 3 \right)$
C. $\left( 4; 7 \right)$
D. $\left( 6; 8 \right)$
A. $\left( 1; 2 \right)$
B. $\left( 2; 3 \right)$
C. $\left( 4; 7 \right)$
D. $\left( 6; 8 \right)$
Diện tích của hình thang cong (H) bằng $S\left( H \right)=\int\limits_{\dfrac{1}{2}}^{2}{\dfrac{1}{x}dx}=\ln x\left| \begin{aligned}
& ^{2} \\
& _{\dfrac{1}{2}} \\
\end{aligned} \right.=\ln 2-\ln \dfrac{1}{2}=2\ln 2$
Diện tích ${{S}_{1}}$ là ${{S}_{1}}=\int\limits_{\dfrac{1}{2}}^{k}{\dfrac{1}{x}dx}=\ln x\left| \begin{aligned}
& ^{k} \\
& _{\dfrac{1}{2}} \\
\end{aligned} \right.=\ln k-\ln \dfrac{1}{2}=\ln k+\ln 2$
Theo giả thiết ta có ${{S}_{1}}=3{{S}_{2}}=3\left( S-{{S}_{1}} \right)\Leftrightarrow {{S}_{1}}=\dfrac{3}{4}S\Leftrightarrow \ln k=\dfrac{\ln 2}{2}\Leftrightarrow k=\sqrt{2}\in \left( 1; 2 \right)$
& ^{2} \\
& _{\dfrac{1}{2}} \\
\end{aligned} \right.=\ln 2-\ln \dfrac{1}{2}=2\ln 2$
Diện tích ${{S}_{1}}$ là ${{S}_{1}}=\int\limits_{\dfrac{1}{2}}^{k}{\dfrac{1}{x}dx}=\ln x\left| \begin{aligned}
& ^{k} \\
& _{\dfrac{1}{2}} \\
\end{aligned} \right.=\ln k-\ln \dfrac{1}{2}=\ln k+\ln 2$
Theo giả thiết ta có ${{S}_{1}}=3{{S}_{2}}=3\left( S-{{S}_{1}} \right)\Leftrightarrow {{S}_{1}}=\dfrac{3}{4}S\Leftrightarrow \ln k=\dfrac{\ln 2}{2}\Leftrightarrow k=\sqrt{2}\in \left( 1; 2 \right)$
Đáp án A.