Google
Câu hỏi: Cho hình nón $\left( N \right)$ có đỉnh là $S$, tâm đường tròn đáy là $O$ và góc ở đỉnh bằng $120{}^\circ $. Một mặt phẳng qua $S$ cắt hình nón $\left( N \right)$ theo thiết diện là tam giác vuông $SAB$. Biết rằng khoảng cách giữa hai đường thẳng $AB$ và $SO$ bằng $4$. Tính thể tích của hình nón $\left( N \right)$ ?
A. $V=36\pi $.
B. $V=48\pi $.
C. $V=64\pi $.
D. $V=16\pi $.
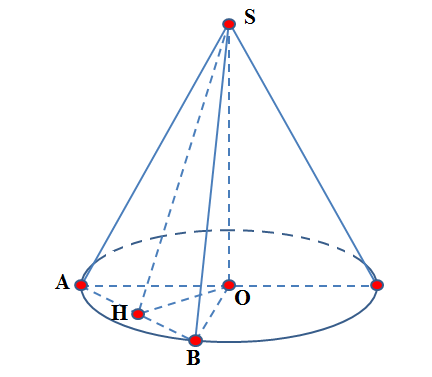Vì góc ở đỉnh bằng $120{}^\circ $ nên ta có $\widehat{ASO}=60{}^\circ .$
Gọi $H$ là trung điểm của $AB$, khi đó $OH$ là đường vuông góc chung của hai đường thẳng $SO$ và $SO$. Như vậy $d\left( SO,AB \right)=OH=4$.
Xét tam giác $SOA$ vuông tại $O$ có $SA=\dfrac{OA}{\sin 60{}^\circ }=\dfrac{2R}{\sqrt{3}}\Rightarrow l=\dfrac{2R}{\sqrt{3}}$.
Xét tam giác $OHB$ vuông tại $H$ có $HB=\sqrt{O{{B}^{2}}-O{{H}^{2}}}=\sqrt{{{R}^{2}}-16}\Rightarrow AB=2HB=2\sqrt{{{R}^{2}}-16}$.
Tam giác $SAB$ vuông cân tại $S$ nên ta có
$AB=l\sqrt{2}\Leftrightarrow 2\sqrt{{{R}^{2}}-16}=\dfrac{2R}{\sqrt{3}}.\sqrt{2}\Leftrightarrow 3\left( {{R}^{2}}-16 \right)=2{{R}^{2}}\Leftrightarrow {{R}^{2}}=48\Leftrightarrow R=4\sqrt{3}\Rightarrow l=8$.
Suy ra $h=\sqrt{{{l}^{2}}-{{R}^{2}}}=\sqrt{{{8}^{2}}-{{\left( 4\sqrt{3} \right)}^{2}}}=4$.
Vậy thể tích của hình nón là $V=\dfrac{1}{3}\pi {{R}^{2}}h=\dfrac{1}{3}\pi .{{\left( 4\sqrt{3} \right)}^{2}}.4=64\pi $.
A. $V=36\pi $.
B. $V=48\pi $.
C. $V=64\pi $.
D. $V=16\pi $.
Gọi $H$ là trung điểm của $AB$, khi đó $OH$ là đường vuông góc chung của hai đường thẳng $SO$ và $SO$. Như vậy $d\left( SO,AB \right)=OH=4$.
Xét tam giác $SOA$ vuông tại $O$ có $SA=\dfrac{OA}{\sin 60{}^\circ }=\dfrac{2R}{\sqrt{3}}\Rightarrow l=\dfrac{2R}{\sqrt{3}}$.
Xét tam giác $OHB$ vuông tại $H$ có $HB=\sqrt{O{{B}^{2}}-O{{H}^{2}}}=\sqrt{{{R}^{2}}-16}\Rightarrow AB=2HB=2\sqrt{{{R}^{2}}-16}$.
Tam giác $SAB$ vuông cân tại $S$ nên ta có
$AB=l\sqrt{2}\Leftrightarrow 2\sqrt{{{R}^{2}}-16}=\dfrac{2R}{\sqrt{3}}.\sqrt{2}\Leftrightarrow 3\left( {{R}^{2}}-16 \right)=2{{R}^{2}}\Leftrightarrow {{R}^{2}}=48\Leftrightarrow R=4\sqrt{3}\Rightarrow l=8$.
Suy ra $h=\sqrt{{{l}^{2}}-{{R}^{2}}}=\sqrt{{{8}^{2}}-{{\left( 4\sqrt{3} \right)}^{2}}}=4$.
Vậy thể tích của hình nón là $V=\dfrac{1}{3}\pi {{R}^{2}}h=\dfrac{1}{3}\pi .{{\left( 4\sqrt{3} \right)}^{2}}.4=64\pi $.
Đáp án C.
