Google
Câu hỏi: Cho hình nón đỉnh $S$ có chiều cao bằng $5$, cắt hình nón bởi mặt phẳng qua $S$ và dây cung $AB$ trên đường tròn đáy sao cho $AB=6$, thiết diện thu được có diện tích bằng $15$. Diện tích xung quanh của hình nón bằng:
A. $25\sqrt{2}\pi $.
B. $4\sqrt{41}\pi $.
C. $25\sqrt{3}\pi $.
D. $3\sqrt{34}\pi $.
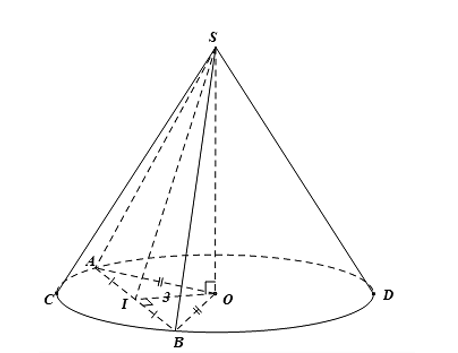Gọi bán kính đường tròn đáy là $R$, khi đó $OI=\sqrt{{{R}^{2}}-I{{A}^{2}}}=\sqrt{{{R}^{2}}-9}$.
Khi đó $SI=\sqrt{O{{I}^{2}}+{{h}^{2}}}=\sqrt{{{R}^{2}}-9+25}=\sqrt{{{R}^{2}}+16}$.
Lại có ${{S}_{SAB}}=15\Leftrightarrow \dfrac{1}{2}AB.SI=15\Leftrightarrow \dfrac{1}{2}.6.\sqrt{{{R}^{2}}+16}=15$ $\Leftrightarrow \sqrt{{{R}^{2}}+16}=5\Leftrightarrow R=3$.
Khi đó độ dài đường sinh là: $l=\sqrt{{{R}^{2}}+{{h}^{2}}}=\sqrt{{{3}^{2}}+{{5}^{2}}}=\sqrt{34}$.
Vậy diện tích xung quanh hình nón là: ${{S}_{xq}}=\pi Rl=\pi .3.\sqrt{34}=3\sqrt{34}\pi $.
A. $25\sqrt{2}\pi $.
B. $4\sqrt{41}\pi $.
C. $25\sqrt{3}\pi $.
D. $3\sqrt{34}\pi $.
Khi đó $SI=\sqrt{O{{I}^{2}}+{{h}^{2}}}=\sqrt{{{R}^{2}}-9+25}=\sqrt{{{R}^{2}}+16}$.
Lại có ${{S}_{SAB}}=15\Leftrightarrow \dfrac{1}{2}AB.SI=15\Leftrightarrow \dfrac{1}{2}.6.\sqrt{{{R}^{2}}+16}=15$ $\Leftrightarrow \sqrt{{{R}^{2}}+16}=5\Leftrightarrow R=3$.
Khi đó độ dài đường sinh là: $l=\sqrt{{{R}^{2}}+{{h}^{2}}}=\sqrt{{{3}^{2}}+{{5}^{2}}}=\sqrt{34}$.
Vậy diện tích xung quanh hình nón là: ${{S}_{xq}}=\pi Rl=\pi .3.\sqrt{34}=3\sqrt{34}\pi $.
Đáp án D.