Câu hỏi: Cho hình nón có thiết diện đi qua đỉnh là tam giác
[/LIST]
A.
B.
C.
D.
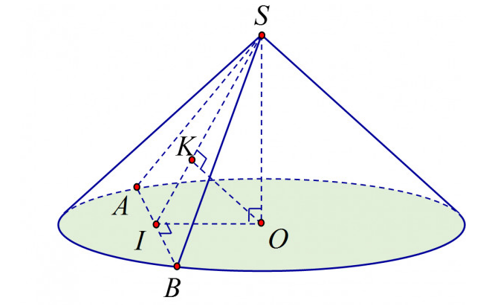 Ta có
Ta có
Mặt khác gọi
Vậy
[/LIST]
A.
B.
C.
D.
Mặt khác gọi
Vậy
Đáp án A.