Câu hỏi: Cho hình lập phương ABCD.MNPQ cạnh bằng a. Tính khoảng cách từ điểm A đến mặt phẳng
A.
B.
C.
D.
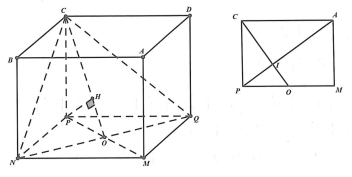
Cách 1 (Tự luận):
Gọi O là tâm hình vuông MNPQ,
Ta có
Do
Ta có
Vậy
Cách 2 (Trắc nghiệm):
Gọi O là tâm hình vuông MNPQ,
Ta thấy PCNQ là tứ diện vuông tại P nên
Suy ra
A.
B.
C.
D.
Cách 1 (Tự luận):
Gọi O là tâm hình vuông MNPQ,
Ta có
Do
Ta có
Vậy
Cách 2 (Trắc nghiệm):
Gọi O là tâm hình vuông MNPQ,
Ta thấy PCNQ là tứ diện vuông tại P nên
Suy ra
Đáp án A.