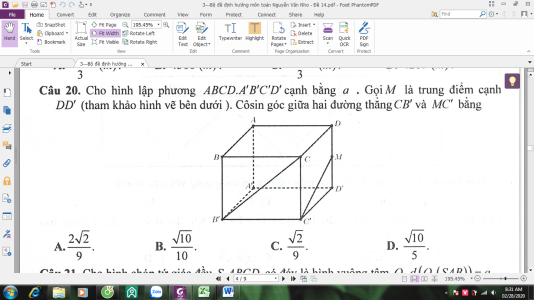
Câu hỏi: Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi M là trung điểm cạnh DD' (tham khảo hình vẽ bên dưới). Côsin góc giữa hai đường thẳng CB' và MC' bằng
A. $\dfrac{2\sqrt{2}}{9}.$
B. $\dfrac{\sqrt{10}}{10}.$
C. $\dfrac{\sqrt{2}}{9}.$
D. $\dfrac{\sqrt{10}}{5}.$

Gọi N là trung điểm của ${A}'{D}'\Rightarrow MN//{A}'D//C{B}'\Rightarrow \left( \widehat{C{B}',M{C}'} \right)=\left( \widehat{MN,M{C}'} \right)=\widehat{NM{C}'}.$
Xét tam giác C'D'M vuông tại D' ta có
$M{C}'=\sqrt{{{a}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}}}=\dfrac{a\sqrt{5}}{2}.$
Xét tam giác C'D'N vuông tại D' ta có
$N{C}'=\sqrt{{{a}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}}}=\dfrac{a\sqrt{5}}{2}.$
Xét tam giác A'D'D có MN là đường trung bình
$\Rightarrow MN=\dfrac{{A}'D}{2}=\dfrac{a\sqrt{2}}{2}.$
Xét tam giác C'MN có
$\cos \widehat{NM{C}'}=\dfrac{M{{N}^{2}}+M{C}'-N{{{{C}'}}^{2}}}{2MN.M{C}'}=\dfrac{\dfrac{{{a}^{2}}}{2}+\dfrac{5{{a}^{2}}}{4}-\dfrac{5{{a}^{2}}}{4}}{2.\dfrac{a\sqrt{2}}{2}.\dfrac{a\sqrt{5}}{2}}=\dfrac{\sqrt{10}}{10}.$

A. $\dfrac{2\sqrt{2}}{9}.$
B. $\dfrac{\sqrt{10}}{10}.$
C. $\dfrac{\sqrt{2}}{9}.$
D. $\dfrac{\sqrt{10}}{5}.$
Gọi N là trung điểm của ${A}'{D}'\Rightarrow MN//{A}'D//C{B}'\Rightarrow \left( \widehat{C{B}',M{C}'} \right)=\left( \widehat{MN,M{C}'} \right)=\widehat{NM{C}'}.$
Xét tam giác C'D'M vuông tại D' ta có
$M{C}'=\sqrt{{{a}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}}}=\dfrac{a\sqrt{5}}{2}.$
Xét tam giác C'D'N vuông tại D' ta có
$N{C}'=\sqrt{{{a}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}}}=\dfrac{a\sqrt{5}}{2}.$
Xét tam giác A'D'D có MN là đường trung bình
$\Rightarrow MN=\dfrac{{A}'D}{2}=\dfrac{a\sqrt{2}}{2}.$
Xét tam giác C'MN có
$\cos \widehat{NM{C}'}=\dfrac{M{{N}^{2}}+M{C}'-N{{{{C}'}}^{2}}}{2MN.M{C}'}=\dfrac{\dfrac{{{a}^{2}}}{2}+\dfrac{5{{a}^{2}}}{4}-\dfrac{5{{a}^{2}}}{4}}{2.\dfrac{a\sqrt{2}}{2}.\dfrac{a\sqrt{5}}{2}}=\dfrac{\sqrt{10}}{10}.$
Đáp án B.