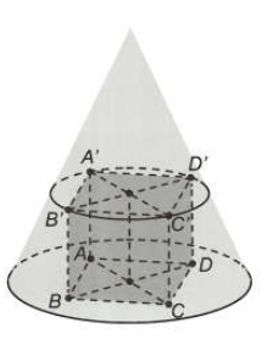
Cho hình lập phương $A B C D \cdot A^{\prime} B^{\prime}...

Xét phần mặt cắt qua trục hình nón và đi qua mặt phẳng ( $\left.\mathrm{AA}^{\prime} \mathrm{C}^{\prime} \mathrm{C}\right)$, kí hiệu như hình vẽ. Với I, $\mathrm{H}$ lần lượt là tâm của hình vuông $A B C D, A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ và đỉnh $A^{\prime}$ nằm trên đường sinh $EF$ của hình nón.
Hình lập phương có thể tích bằng 1 nên $\mathrm{AA}^{\prime}=H I=1, A^{\prime} H=\dfrac{\sqrt{2}}{2}$
Đặt $E H=x(x>0)$. Khi đó, ta có $\dfrac{E H}{E I}=\dfrac{A^{\prime} H}{F I} \Leftrightarrow \dfrac{x}{x+1}=\dfrac{\sqrt{2}}{2 F I} \rightarrow F I=\dfrac{\sqrt{2}}{2}\left(\dfrac{x+1}{x}\right)=r$
Thể tích khối nón $(\mathrm{N})$ là $V_{(N)}=\dfrac{1}{3} \pi r^2 E I=\dfrac{1}{6} \pi\left(\dfrac{x+1}{x}\right)^2(x+1)=\dfrac{\pi}{6} \dfrac{(x+1)^3}{x^2}$
Xét hàm số $f(x)=\dfrac{{{(x+1)}^{3}}}{{{x}^{2}}},\forall x\in (0;+\infty )$. Ta có $f^{\prime}(x)=\dfrac{(x-2)(x+1)^2}{x^3}$
Lập bảng biến thiên
Ta được $\min _{(0 ;+\infty)} f(x)=\dfrac{27}{4}$ tại x $=2$. Suy ra $\min V_{(N)}=\dfrac{9 \pi}{8}$