Google
Câu hỏi: Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$, $AB=\sqrt{2}a$, góc giữa mặt phẳng $\left( A'BC \right)$ và mặt phẳng $\left( ABC \right)$ bằng ${{60}^{0}}$. Thể tích khối lăng trụ đã cho bằng
A. $3{{a}^{3}}$.
B. $3\sqrt{3}{{a}^{3}}$.
C. $\sqrt{3}{{a}^{3}}$.
D. ${{a}^{3}}$.
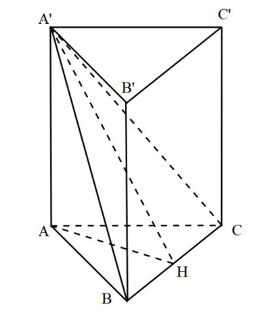Gọi H là trung điểm của $BC$. Dễ thấy $\angle A'HA={{60}^{0}}$ là góc giữa $mp\left( A'BC \right)$ và $mp\left( ABC \right)$
Ta có, $AA'=AH.\tan {{60}^{0}}=\dfrac{1}{2}BC.\tan {{60}^{0}}=a\sqrt{3}$ ; ${{S}_{\Delta ABC}}=\dfrac{1}{2}{{\left( \sqrt{2}a \right)}^{2}}={{a}^{2}}$
Vậy ${{V}_{ABC.A'B'C'}}=AA'.{{S}_{\Delta ABC}}=\sqrt{3}{{a}^{3}}$.
A. $3{{a}^{3}}$.
B. $3\sqrt{3}{{a}^{3}}$.
C. $\sqrt{3}{{a}^{3}}$.
D. ${{a}^{3}}$.
Ta có, $AA'=AH.\tan {{60}^{0}}=\dfrac{1}{2}BC.\tan {{60}^{0}}=a\sqrt{3}$ ; ${{S}_{\Delta ABC}}=\dfrac{1}{2}{{\left( \sqrt{2}a \right)}^{2}}={{a}^{2}}$
Vậy ${{V}_{ABC.A'B'C'}}=AA'.{{S}_{\Delta ABC}}=\sqrt{3}{{a}^{3}}$.
Đáp án C.