Google
Câu hỏi: Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}'$ có $AB=A{A}'=2a$, $AC=a$, $\widehat{BAC}=120{}^\circ $. Bán kính mặt cầu ngoại tiếp hình chóp $A.BC{C}'{B}'$ bằng
A. $\dfrac{\sqrt{30}a}{3}$.
B. $\dfrac{\sqrt{10}a}{3}$.
C. $\dfrac{\sqrt{30}a}{10}$.
D. $\dfrac{\sqrt{33}a}{3}$.
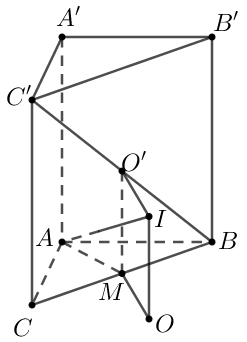Gọi ${O}'$ là tâm hình chữ nhật $BC{C}'{B}'$. Từ ${O}'$ kẻ đường thẳng $\Delta $ vuông góc với $\left( BC{C}'{B}' \right)$ thì $\Delta $ là trục đường tròn ngoại tiếp $BC{C}'{B}'$.
Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Từ $O$ kẻ đường thẳng ${\Delta }'$ vuông góc với $\left( ABC \right)$ (song song với $B{B}'$ ), cắt $\Delta $ tại $I$.
Khi đó $I$ là tâm mặt cầu ngoại tiếp $A.BC{C}'{B}'$, bán kính mặt cầu ngoại tiếp là $R=IA$.
Xét tam giác $IOA$ vuông tại $O$ (vì $IO\bot \left( ABC \right)$ ) nên $IA=\sqrt{I{{O}^{2}}+O{{A}^{2}}}$.
Trong đó $IO={O}'M=\dfrac{1}{2}B{B}'=\dfrac{1}{2}A{A}'=a$, với $M$ là trung điểm $BC$ ;
Bán kính đường tròn ngoại tiếp tam giác $ABC$
$O{{A}^{2}}=\dfrac{B{{C}^{2}}}{4{{\sin }^{2}}\widehat{BAC}}=\dfrac{A{{B}^{2}}+A{{C}^{2}}-2AB\cdot AC\cdot \cos \widehat{BAC}}{4{{\sin }^{2}}\widehat{BAC}}=\dfrac{4{{a}^{2}}+{{a}^{2}}-2\cdot 2a\cdot a\cdot \cos 120{}^\circ }{4{{\sin }^{2}}120{}^\circ }=\dfrac{7{{a}^{2}}}{3}$.
Suy ra $IA=\sqrt{I{{O}^{2}}+O{{A}^{2}}}=\sqrt{{{a}^{2}}+\dfrac{7{{a}^{2}}}{3}}=\dfrac{\sqrt{30}a}{3}$.
A. $\dfrac{\sqrt{30}a}{3}$.
B. $\dfrac{\sqrt{10}a}{3}$.
C. $\dfrac{\sqrt{30}a}{10}$.
D. $\dfrac{\sqrt{33}a}{3}$.
Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Từ $O$ kẻ đường thẳng ${\Delta }'$ vuông góc với $\left( ABC \right)$ (song song với $B{B}'$ ), cắt $\Delta $ tại $I$.
Khi đó $I$ là tâm mặt cầu ngoại tiếp $A.BC{C}'{B}'$, bán kính mặt cầu ngoại tiếp là $R=IA$.
Xét tam giác $IOA$ vuông tại $O$ (vì $IO\bot \left( ABC \right)$ ) nên $IA=\sqrt{I{{O}^{2}}+O{{A}^{2}}}$.
Trong đó $IO={O}'M=\dfrac{1}{2}B{B}'=\dfrac{1}{2}A{A}'=a$, với $M$ là trung điểm $BC$ ;
Bán kính đường tròn ngoại tiếp tam giác $ABC$
$O{{A}^{2}}=\dfrac{B{{C}^{2}}}{4{{\sin }^{2}}\widehat{BAC}}=\dfrac{A{{B}^{2}}+A{{C}^{2}}-2AB\cdot AC\cdot \cos \widehat{BAC}}{4{{\sin }^{2}}\widehat{BAC}}=\dfrac{4{{a}^{2}}+{{a}^{2}}-2\cdot 2a\cdot a\cdot \cos 120{}^\circ }{4{{\sin }^{2}}120{}^\circ }=\dfrac{7{{a}^{2}}}{3}$.
Suy ra $IA=\sqrt{I{{O}^{2}}+O{{A}^{2}}}=\sqrt{{{a}^{2}}+\dfrac{7{{a}^{2}}}{3}}=\dfrac{\sqrt{30}a}{3}$.
Đáp án A.