Câu hỏi: Cho hình hộp chữ nhật
A.
B.
C.
D.
A.
B.
C.
D.
Cách 1. Gọi
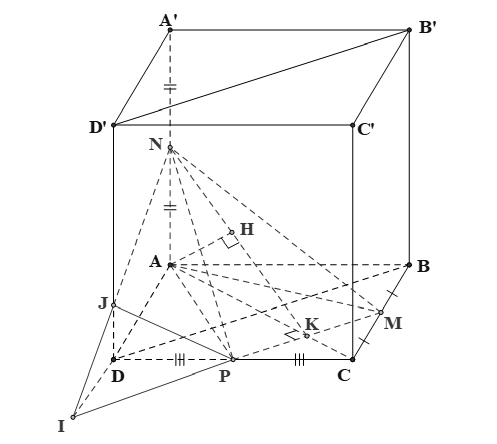 Ta có
Ta có
Lại có
Mặt khác
Dễ thấy
Suy ra
Vậy
Cách 2. Đặt các trục
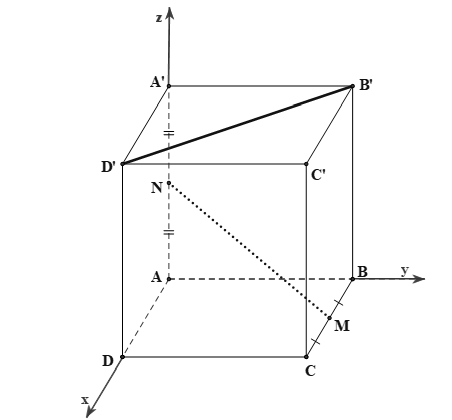 Chọn
Chọn
Ta có
Khi đó
Lại có
Mặt khác
Dễ thấy
Suy ra
Vậy
Cách 2. Đặt các trục
Ta có
Khi đó
Đáp án A.