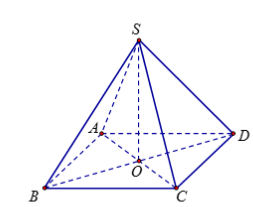
Câu hỏi: Cho hình chóp tứ giác đều S.ABCDcó cạnh đáy bằng 2a, cạnh bên bằng 3a. Tính thể tích Vcủa khối chóp đã cho.
A. $V=\dfrac{4{{a}^{3}}}{3}$.
B. $V=4\sqrt{7}{{a}^{3}}$.
C. $V=\dfrac{4\sqrt{7{{a}^{3}}}}{9}$.
D. $V=\dfrac{4\sqrt{7{{a}^{3}}}}{3}$

A. $V=\dfrac{4{{a}^{3}}}{3}$.
B. $V=4\sqrt{7}{{a}^{3}}$.
C. $V=\dfrac{4\sqrt{7{{a}^{3}}}}{9}$.
D. $V=\dfrac{4\sqrt{7{{a}^{3}}}}{3}$
Phương pháp:
Áp dụng công thức tính thể tích hình chóp ${{V}_{chop}}=\dfrac{1}{3}{{S}_{day}}.h$.
Cách giải:
Gọi $O=AC\cap BD\Rightarrow SO\bot \left( ABCD \right)$.
Khi đó ta có $AO=\dfrac{AC}{2}=\dfrac{2a\sqrt{2}}{2}=a\sqrt{2}$
Xét tam giác SAOvuông tại Ocó $AO=a\sqrt{2};SA=3a$.
Áp dụng định lí Pytago ta có: $SO=\sqrt{S{{A}^{2}}-A{{O}^{2}}}=\sqrt{{{\left( 3a \right)}^{2}}-{{\left( a\sqrt{2} \right)}^{2}}}=a\sqrt{7}$.
Diện tích hình vuông ABCDlà ${{S}_{ABCD}}=\left( 2{{a}^{2}} \right)=4{{a}^{2}}$
Vậy ${{S}_{ABCD}}=\dfrac{1}{3}\text{.}SO.{{S}_{ABCD}}=\dfrac{1}{3}a\sqrt{7.}4{{a}^{2}}=\dfrac{4\sqrt{7}{{a}^{3}}}{3}$
Áp dụng công thức tính thể tích hình chóp ${{V}_{chop}}=\dfrac{1}{3}{{S}_{day}}.h$.
Cách giải:
Gọi $O=AC\cap BD\Rightarrow SO\bot \left( ABCD \right)$.
Khi đó ta có $AO=\dfrac{AC}{2}=\dfrac{2a\sqrt{2}}{2}=a\sqrt{2}$
Xét tam giác SAOvuông tại Ocó $AO=a\sqrt{2};SA=3a$.
Áp dụng định lí Pytago ta có: $SO=\sqrt{S{{A}^{2}}-A{{O}^{2}}}=\sqrt{{{\left( 3a \right)}^{2}}-{{\left( a\sqrt{2} \right)}^{2}}}=a\sqrt{7}$.
Diện tích hình vuông ABCDlà ${{S}_{ABCD}}=\left( 2{{a}^{2}} \right)=4{{a}^{2}}$
Vậy ${{S}_{ABCD}}=\dfrac{1}{3}\text{.}SO.{{S}_{ABCD}}=\dfrac{1}{3}a\sqrt{7.}4{{a}^{2}}=\dfrac{4\sqrt{7}{{a}^{3}}}{3}$
Đáp án D.