Google
Câu hỏi: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và cạnh bên bằng $\sqrt{2}a$ (tham khảo hình vẽ).
Góc giữa đường thẳng $SB$ và mặt phẳng $\left( SAC \right)$ bằng
A. ${{45}^{o}}$.
B. ${{90}^{o}}$.
C. ${{30}^{o}}$.
D. ${{60}^{o}}$.
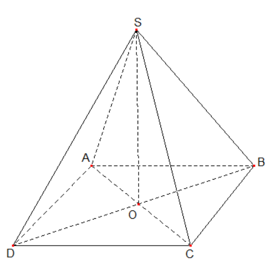Hình chóp tứ giác đều $S.ABCD$ nên đáy $ABCD$ là hình vuông
Gọi $O$ là tâm của đáy $\Rightarrow SO\bot \left( ABCD \right)$
Ta có $SA=a\sqrt{2},AB=a$, $BD=a\sqrt{2}$ $\Rightarrow BO=\dfrac{a\sqrt{2}}{2}$
Ta có $\left\{ \begin{aligned}
& BO\bot AC \\
& BO\bot SO \\
\end{aligned} \right.\Rightarrow BO\bot \left( SAC \right)$
$O$ là hình chiếu của $B$ lên $\left( SAC \right)$ $\Rightarrow \left( SB,\left( SAC \right) \right)=\widehat{BSO}$
Xét $\Delta SBO$ vuông tại $O$, có: $\text{sin}\widehat{BSO}=\dfrac{OB}{SB}=\dfrac{\dfrac{a\sqrt{2}}{2}}{a\sqrt{2}}=\dfrac{1}{2}\Rightarrow \widehat{SBO}={{30}^{o}}$
A. ${{45}^{o}}$.
B. ${{90}^{o}}$.
C. ${{30}^{o}}$.
D. ${{60}^{o}}$.
Gọi $O$ là tâm của đáy $\Rightarrow SO\bot \left( ABCD \right)$
Ta có $SA=a\sqrt{2},AB=a$, $BD=a\sqrt{2}$ $\Rightarrow BO=\dfrac{a\sqrt{2}}{2}$
Ta có $\left\{ \begin{aligned}
& BO\bot AC \\
& BO\bot SO \\
\end{aligned} \right.\Rightarrow BO\bot \left( SAC \right)$
$O$ là hình chiếu của $B$ lên $\left( SAC \right)$ $\Rightarrow \left( SB,\left( SAC \right) \right)=\widehat{BSO}$
Xét $\Delta SBO$ vuông tại $O$, có: $\text{sin}\widehat{BSO}=\dfrac{OB}{SB}=\dfrac{\dfrac{a\sqrt{2}}{2}}{a\sqrt{2}}=\dfrac{1}{2}\Rightarrow \widehat{SBO}={{30}^{o}}$
Đáp án C.