Google
Câu hỏi: Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $2a$, khoảng cách từ tâm $O$ của đường tròn ngoại tiếp tam giác đáy $ABC$ đến một mặt bên là $\dfrac{a}{2}$. Thể tích của khối nón ngoại tiếp hình chóp $S.ABC$ bằng
A. $\dfrac{2\pi {{a}^{3}}}{3}$.
B. $\dfrac{4\pi {{a}^{3}}}{9}$.
C. $\dfrac{4\pi {{a}^{3}}}{3}$.
D. $\dfrac{4\pi {{a}^{3}}}{27}$.
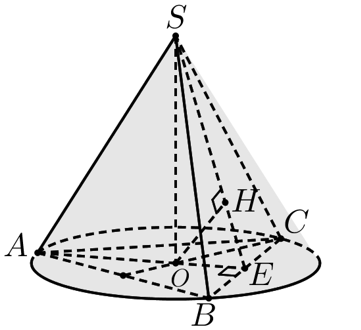Gọi $E$ là trung điểm của $BC$, suy ra $BC\bot OE$. Dựng $OH\bot SE$ tại $H$.
Ta có $\left\{ \begin{aligned}
& BC\bot OE \\
& BC\bot SO \\
\end{aligned} \right.\Rightarrow BC\bot \left( SOE \right)\Rightarrow BC\bot OH$.
Khi đó $\left\{ \begin{aligned}
& OH\bot BC \\
& OH\bot SE \\
\end{aligned} \right.\Rightarrow OH\bot \left( SBC \right) $, suy ra $ OH=d\left( O , \left( SBC \right) \right)=\dfrac{a}{2}$.
Vì tam giác đều $ABC$ cạnh $2a$ nên $AE=2a.\dfrac{\sqrt{3}}{2}=a\sqrt{3}$.
Suy ra $OA=\dfrac{2}{3}AE=\dfrac{2a\sqrt{3}}{3}$ và $OE=\dfrac{1}{3}AE=\dfrac{a\sqrt{3}}{3}$.
Trong tam giác vuông $SOE,$ ta có: $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{O{{E}^{2}}}+\dfrac{1}{S{{O}^{2}}}\Rightarrow \dfrac{1}{S{{O}^{2}}}=\dfrac{1}{O{{H}^{2}}}-\dfrac{1}{O{{E}^{2}}}=\dfrac{1}{{{a}^{2}}}\Rightarrow SO=a.$
Khối nón ngoại tiếp hình chóp $S.ABC$ có bán kính đáy $R=OA=\dfrac{2a\sqrt{3}}{3}$, đường cao $h=SO=a$.
Vậy thể tích khối nón: $V=\dfrac{1}{3}\pi {{R}^{2}}.h=\dfrac{1}{3}\pi {{\left( \dfrac{2a\sqrt{3}}{3} \right)}^{2}}.a=\dfrac{4\pi {{a}^{3}}}{9}$.
A. $\dfrac{2\pi {{a}^{3}}}{3}$.
B. $\dfrac{4\pi {{a}^{3}}}{9}$.
C. $\dfrac{4\pi {{a}^{3}}}{3}$.
D. $\dfrac{4\pi {{a}^{3}}}{27}$.
Ta có $\left\{ \begin{aligned}
& BC\bot OE \\
& BC\bot SO \\
\end{aligned} \right.\Rightarrow BC\bot \left( SOE \right)\Rightarrow BC\bot OH$.
Khi đó $\left\{ \begin{aligned}
& OH\bot BC \\
& OH\bot SE \\
\end{aligned} \right.\Rightarrow OH\bot \left( SBC \right) $, suy ra $ OH=d\left( O , \left( SBC \right) \right)=\dfrac{a}{2}$.
Vì tam giác đều $ABC$ cạnh $2a$ nên $AE=2a.\dfrac{\sqrt{3}}{2}=a\sqrt{3}$.
Suy ra $OA=\dfrac{2}{3}AE=\dfrac{2a\sqrt{3}}{3}$ và $OE=\dfrac{1}{3}AE=\dfrac{a\sqrt{3}}{3}$.
Trong tam giác vuông $SOE,$ ta có: $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{O{{E}^{2}}}+\dfrac{1}{S{{O}^{2}}}\Rightarrow \dfrac{1}{S{{O}^{2}}}=\dfrac{1}{O{{H}^{2}}}-\dfrac{1}{O{{E}^{2}}}=\dfrac{1}{{{a}^{2}}}\Rightarrow SO=a.$
Khối nón ngoại tiếp hình chóp $S.ABC$ có bán kính đáy $R=OA=\dfrac{2a\sqrt{3}}{3}$, đường cao $h=SO=a$.
Vậy thể tích khối nón: $V=\dfrac{1}{3}\pi {{R}^{2}}.h=\dfrac{1}{3}\pi {{\left( \dfrac{2a\sqrt{3}}{3} \right)}^{2}}.a=\dfrac{4\pi {{a}^{3}}}{9}$.
Đáp án B.
