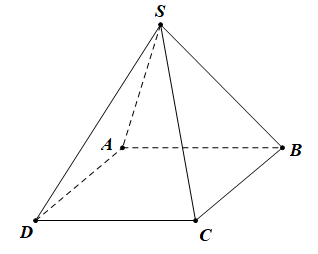
Câu hỏi: Cho hình chóp $S.ABCD$ có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa hai đường thẳng $SC$ và $AB$ bằng
A. ${{90}^{0}}$.
B. ${{60}^{0}}$.
C. ${{30}^{0}}$.
D. ${{45}^{0}}$.

Từ giả thiết ta có $AB \text{//} CD$ nên $\left( \widehat{SC,AB} \right)=\left( \widehat{SC,CD} \right)$.
Mặt khác, hình chóp có tất cả các cạnh bằng nhau nên tam giác $SCD$ đều.
Suy ra $\left( \widehat{SC,AB} \right)=\left( \widehat{SC,CD} \right)=\widehat{SCD}={{60}^{0}}$.
Vậy góc giữa hai đường thẳng $SC$ và $AB$ bằng ${{60}^{0}}$.
A. ${{90}^{0}}$.
B. ${{60}^{0}}$.
C. ${{30}^{0}}$.
D. ${{45}^{0}}$.
Từ giả thiết ta có $AB \text{//} CD$ nên $\left( \widehat{SC,AB} \right)=\left( \widehat{SC,CD} \right)$.
Mặt khác, hình chóp có tất cả các cạnh bằng nhau nên tam giác $SCD$ đều.
Suy ra $\left( \widehat{SC,AB} \right)=\left( \widehat{SC,CD} \right)=\widehat{SCD}={{60}^{0}}$.
Vậy góc giữa hai đường thẳng $SC$ và $AB$ bằng ${{60}^{0}}$.
Đáp án B.