Google
Câu hỏi: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, đường thẳng $SA$ vuông góc với mặt phẳng $\left( ABCD \right),SA=a\sqrt{2}$. Khoảng cách giữa hai đường thẳng $SB$ và $AD$ bằng
A. $\dfrac{a\sqrt{6}}{3}$.
B. $\dfrac{a\sqrt{2}}{3}$.
C. $\dfrac{a\sqrt{3}}{2}$.
D. $a$.
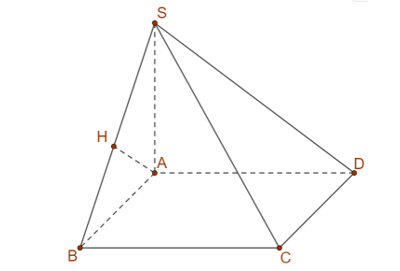Ta có $d\left( SB,AD \right)=d\left( AD,\left( SBC \right) \right)=d\left( A,\left( SBC \right) \right)$.
Do $BC\bot \left( SAB \right)$, kẻ $AH\bot SB\Rightarrow AH\bot BC$. Do đó $AH\bot \left( SBC \right)\Rightarrow d\left( A,\left( SBC \right) \right)=AH$.
Ta có $AH=\dfrac{SA.AB}{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}=\dfrac{\sqrt{2}a}{\sqrt{3}}=\dfrac{a\sqrt{6}}{3}$.
A. $\dfrac{a\sqrt{6}}{3}$.
B. $\dfrac{a\sqrt{2}}{3}$.
C. $\dfrac{a\sqrt{3}}{2}$.
D. $a$.
Do $BC\bot \left( SAB \right)$, kẻ $AH\bot SB\Rightarrow AH\bot BC$. Do đó $AH\bot \left( SBC \right)\Rightarrow d\left( A,\left( SBC \right) \right)=AH$.
Ta có $AH=\dfrac{SA.AB}{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}=\dfrac{\sqrt{2}a}{\sqrt{3}}=\dfrac{a\sqrt{6}}{3}$.
Đáp án A.