Google
Câu hỏi: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $2a,$ hình chiếu vuông góc của $S$ lên đáy là trung điểm cạnh $AB$, $\widehat{ASB}=90{}^\circ $. Khoảng cách từ $C$ đến mặt phẳng $\left( SBD \right)$ bằng
A. $\dfrac{2\sqrt{6}a}{3}$.
B. $\dfrac{\sqrt{6}a}{3}$.
C. $\dfrac{\sqrt{3}a}{3}$
D. $\dfrac{2\sqrt{3}a}{3}$.
B. $\dfrac{\sqrt{6}a}{3}$.
C. $\dfrac{\sqrt{3}a}{3}$
D. $\dfrac{2\sqrt{3}a}{3}$.
Ta có hình vẽ minh họa sau:
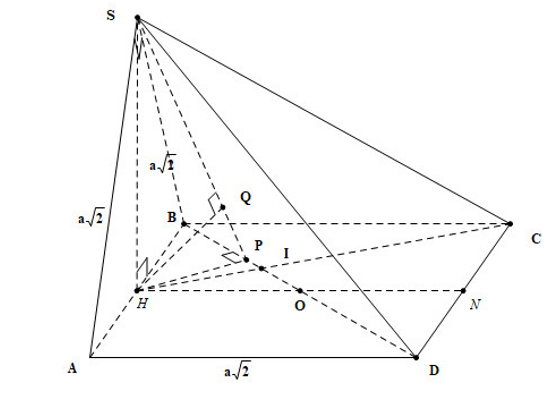Gọi $H$ là hình chiếu vuông góc của $S$ lên đáy $\Rightarrow SH\bot \left( ABCD \right)\Rightarrow SH\bot AB$
Xét $\Delta SAB$ vuông tại $S$ có $SH$ là đường cao đồng thời là đường trung tuyến
$\Rightarrow \Delta SAB$ vuông cân tại $S$ $\Rightarrow SH=\dfrac{1}{2}AB=a$
Gọi $N$ là trung điểm của cạnh $CD$, $HN\cap BD=\left\{ O \right\}$, $HC\cap BD=\left\{ I \right\}$
Ta có $OH//BC$, theo định lý Thales $\dfrac{IH}{IC}=\dfrac{OH}{BC}=\dfrac{1}{2}\Rightarrow \dfrac{IH}{IC}=\dfrac{1}{2}$
Lại có $HC\cap \left( SBD \right)=\left\{ I \right\}\Rightarrow \dfrac{d\left( H;\left( SBD \right) \right)}{d\left( C;\left( SBD \right) \right)}=\dfrac{IH}{IC}=\dfrac{1}{2}\Rightarrow d\left( C;\left( SBD \right) \right)=2d\left( H;\left( SBD \right) \right)$
Trong mặt phẳng $\left( ABCD \right)$, từ $H$ kẻ $HP\bot BD$ tại $P$ $\left( 1 \right)$
Do $SH\bot \left( ABCD \right)\Rightarrow SH\bot BD \left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ $\Rightarrow BD\bot \left( SHP \right) \left( 3 \right)$. Mặt khác $BD\subset \left( SBD \right) \left( 4 \right)$
Từ $\left( 3 \right)$ và $\left( 4 \right)$ $\Rightarrow \left( SHP \right)\bot \left( SBD \right)$ theo giao tuyến $SP$
Trong mặt phẳng $\left( SHP \right)$, hạ $HQ\bot SP$ tại $Q$ $\Rightarrow HQ\bot \left( SBD \right)\Rightarrow d\left( H;\left( SBD \right) \right)=HQ$
Xét $\Delta HPB$ vuông tại $P$, có $\sin \widehat{HBP}=\dfrac{HP}{HB}\Rightarrow HP=HB.\sin 45{}^\circ =\dfrac{a\sqrt{2}}{2}$
Xét $\Delta SHP$ vuông tại $H$, có đường cao $HQ$ $\Rightarrow HQ=\dfrac{HS.HP}{\sqrt{H{{S}^{2}}+H{{P}^{2}}}}=\dfrac{a\sqrt{3}}{3}$
$\Rightarrow d\left( C;\left( SBD \right) \right)=2d\left( H;\left( SBD \right) \right)=2HQ=\dfrac{2\sqrt{3}a}{3}$.
Xét $\Delta SAB$ vuông tại $S$ có $SH$ là đường cao đồng thời là đường trung tuyến
$\Rightarrow \Delta SAB$ vuông cân tại $S$ $\Rightarrow SH=\dfrac{1}{2}AB=a$
Gọi $N$ là trung điểm của cạnh $CD$, $HN\cap BD=\left\{ O \right\}$, $HC\cap BD=\left\{ I \right\}$
Ta có $OH//BC$, theo định lý Thales $\dfrac{IH}{IC}=\dfrac{OH}{BC}=\dfrac{1}{2}\Rightarrow \dfrac{IH}{IC}=\dfrac{1}{2}$
Lại có $HC\cap \left( SBD \right)=\left\{ I \right\}\Rightarrow \dfrac{d\left( H;\left( SBD \right) \right)}{d\left( C;\left( SBD \right) \right)}=\dfrac{IH}{IC}=\dfrac{1}{2}\Rightarrow d\left( C;\left( SBD \right) \right)=2d\left( H;\left( SBD \right) \right)$
Trong mặt phẳng $\left( ABCD \right)$, từ $H$ kẻ $HP\bot BD$ tại $P$ $\left( 1 \right)$
Do $SH\bot \left( ABCD \right)\Rightarrow SH\bot BD \left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ $\Rightarrow BD\bot \left( SHP \right) \left( 3 \right)$. Mặt khác $BD\subset \left( SBD \right) \left( 4 \right)$
Từ $\left( 3 \right)$ và $\left( 4 \right)$ $\Rightarrow \left( SHP \right)\bot \left( SBD \right)$ theo giao tuyến $SP$
Trong mặt phẳng $\left( SHP \right)$, hạ $HQ\bot SP$ tại $Q$ $\Rightarrow HQ\bot \left( SBD \right)\Rightarrow d\left( H;\left( SBD \right) \right)=HQ$
Xét $\Delta HPB$ vuông tại $P$, có $\sin \widehat{HBP}=\dfrac{HP}{HB}\Rightarrow HP=HB.\sin 45{}^\circ =\dfrac{a\sqrt{2}}{2}$
Xét $\Delta SHP$ vuông tại $H$, có đường cao $HQ$ $\Rightarrow HQ=\dfrac{HS.HP}{\sqrt{H{{S}^{2}}+H{{P}^{2}}}}=\dfrac{a\sqrt{3}}{3}$
$\Rightarrow d\left( C;\left( SBD \right) \right)=2d\left( H;\left( SBD \right) \right)=2HQ=\dfrac{2\sqrt{3}a}{3}$.
Đáp án D.