Câu hỏi: Cho hình chóp
A.
B.
C.
D.
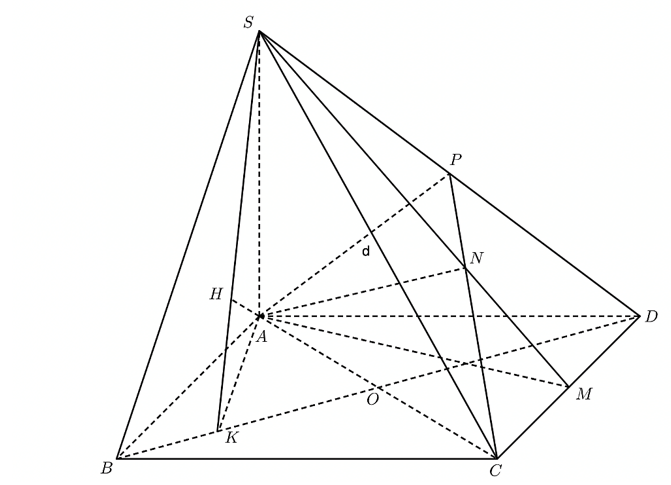 Áp dụng định lý Menelaus cho tam giác
Áp dụng định lý Menelaus cho tam giác
Gọi
Ta có:
Mặt khác:
Ta có:
Mặt khác:
A.
B.
C.
D.
Gọi
Ta có:
Mặt khác:
Ta có:
Mặt khác:
Đáp án D.