Google
Câu hỏi: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a,$ $SA=a\sqrt{3}$ và $SA$ vuông góc với mặt phẳng đáy. Mặt phẳng $\left( P \right)$ đi qua điểm $A$ và vuông góc với $SC$ cắt $SB,$ $SC,$ $SD$ lần lượt tại ${B}',$ ${C}',$ ${D}'.$ Thể tích khối chóp $S.A{B}'{C}'{D}'$ bằng
A. $\dfrac{3\sqrt{3}{{a}^{3}}}{20}$.
B. $\dfrac{9\sqrt{3}{{a}^{3}}}{20}$.
C. $\dfrac{3\sqrt{3}{{a}^{3}}}{10}$.
D. $\dfrac{3\sqrt{3}{{a}^{3}}}{40}$.
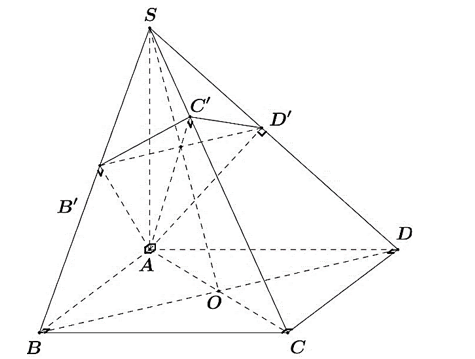Ta có: ${{V}_{S.ABCD}}=\dfrac{1}{3}.a\sqrt{3}.{{a}^{2}}$. Do $A{C}'\bot SC \left( do SC\bot \left( P \right), A{C}'\subset \left( P \right) \right).$
$\left\{ \begin{aligned}
& A{D}'\bot SC \left( do SC\bot \left( P \right), A{D}'\subset \left( P \right) \right) \\
& A{D}'\bot CD\left( do CD\bot AD, CD\bot SA \right) \\
\end{aligned} \right.\Rightarrow A{D}'\bot SD.$
$\left\{ \begin{aligned}
& A{B}'\bot SC \left( do SC\bot \left( P \right), A{B}'\subset \left( P \right) \right) \\
& A{B}'\bot BC\left( do BC\bot AB, BC\bot SA \right) \\
\end{aligned} \right.\Rightarrow A{B}'\bot SB.$
Trong $\Delta SAB$ vuông tại $A$ có: $S{{A}^{2}}=S{B}'.SB\Rightarrow \dfrac{S{B}'}{SB}=\dfrac{S{{A}^{2}}}{S{{B}^{2}}}=\dfrac{3}{4}.$
Trong $\Delta SAD$ vuông tại $A$ có: $S{{A}^{2}}=SD'.SD\Rightarrow \dfrac{S{D}'}{SD}=\dfrac{S{{A}^{2}}}{S{{D}^{2}}}=\dfrac{3}{4}.$
Trong $\Delta SAC$ vuông tại $A$ có: $S{{A}^{2}}=S{C}'.SC\Rightarrow \dfrac{S{C}'}{SC}=\dfrac{S{{A}^{2}}}{S{{C}^{2}}}=\dfrac{3}{5}.$
$\dfrac{{{V}_{S.A{B}'{C}'}}}{{{V}_{S.ABC}}}=\dfrac{S{B}'}{SB}.\dfrac{S{C}'}{SC}=\dfrac{9}{20}$ và $\dfrac{{{V}_{S.A{C}'{D}'}}}{{{V}_{S.ACD}}}=\dfrac{S{C}'}{SC}.\dfrac{S{D}'}{SD}=\dfrac{9}{20}.$
$\Rightarrow \dfrac{{{V}_{S.A{B}'{C}'}}}{{{V}_{S.ABC}}}+\dfrac{{{V}_{S.A{C}'{D}'}}}{{{V}_{S.ACD}}}=\dfrac{{{V}_{S.A{B}'{C}'}}+{{V}_{S.A{C}'{D}'}}}{{{V}_{S.ABC}}}=\dfrac{{{V}_{S.A{B}'{C}'D'}}}{{{V}_{S.ABC}}}=\dfrac{2.{{V}_{S.A{B}'{C}'D'}}}{{{V}_{S.ABCD}}}=\dfrac{9}{10}.$
Vậy ${{V}_{S.A{B}'{C}'D'}}=\dfrac{9}{20}.{{V}_{S.ABCD}}=\dfrac{3\sqrt{3}{{a}^{3}}}{20}$.
A. $\dfrac{3\sqrt{3}{{a}^{3}}}{20}$.
B. $\dfrac{9\sqrt{3}{{a}^{3}}}{20}$.
C. $\dfrac{3\sqrt{3}{{a}^{3}}}{10}$.
D. $\dfrac{3\sqrt{3}{{a}^{3}}}{40}$.
$\left\{ \begin{aligned}
& A{D}'\bot SC \left( do SC\bot \left( P \right), A{D}'\subset \left( P \right) \right) \\
& A{D}'\bot CD\left( do CD\bot AD, CD\bot SA \right) \\
\end{aligned} \right.\Rightarrow A{D}'\bot SD.$
$\left\{ \begin{aligned}
& A{B}'\bot SC \left( do SC\bot \left( P \right), A{B}'\subset \left( P \right) \right) \\
& A{B}'\bot BC\left( do BC\bot AB, BC\bot SA \right) \\
\end{aligned} \right.\Rightarrow A{B}'\bot SB.$
Trong $\Delta SAB$ vuông tại $A$ có: $S{{A}^{2}}=S{B}'.SB\Rightarrow \dfrac{S{B}'}{SB}=\dfrac{S{{A}^{2}}}{S{{B}^{2}}}=\dfrac{3}{4}.$
Trong $\Delta SAD$ vuông tại $A$ có: $S{{A}^{2}}=SD'.SD\Rightarrow \dfrac{S{D}'}{SD}=\dfrac{S{{A}^{2}}}{S{{D}^{2}}}=\dfrac{3}{4}.$
Trong $\Delta SAC$ vuông tại $A$ có: $S{{A}^{2}}=S{C}'.SC\Rightarrow \dfrac{S{C}'}{SC}=\dfrac{S{{A}^{2}}}{S{{C}^{2}}}=\dfrac{3}{5}.$
$\dfrac{{{V}_{S.A{B}'{C}'}}}{{{V}_{S.ABC}}}=\dfrac{S{B}'}{SB}.\dfrac{S{C}'}{SC}=\dfrac{9}{20}$ và $\dfrac{{{V}_{S.A{C}'{D}'}}}{{{V}_{S.ACD}}}=\dfrac{S{C}'}{SC}.\dfrac{S{D}'}{SD}=\dfrac{9}{20}.$
$\Rightarrow \dfrac{{{V}_{S.A{B}'{C}'}}}{{{V}_{S.ABC}}}+\dfrac{{{V}_{S.A{C}'{D}'}}}{{{V}_{S.ACD}}}=\dfrac{{{V}_{S.A{B}'{C}'}}+{{V}_{S.A{C}'{D}'}}}{{{V}_{S.ABC}}}=\dfrac{{{V}_{S.A{B}'{C}'D'}}}{{{V}_{S.ABC}}}=\dfrac{2.{{V}_{S.A{B}'{C}'D'}}}{{{V}_{S.ABCD}}}=\dfrac{9}{10}.$
Vậy ${{V}_{S.A{B}'{C}'D'}}=\dfrac{9}{20}.{{V}_{S.ABCD}}=\dfrac{3\sqrt{3}{{a}^{3}}}{20}$.
Đáp án A.