Câu hỏi: Cho hình chóp
A.
B.
C.
D.
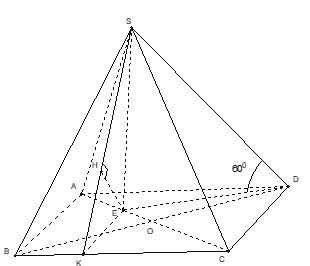
Đặc điểm hình: Góc giữa
Xác định khoảng cách
Tính
A.
B.
C.
D.
Đặc điểm hình: Góc giữa
Xác định khoảng cách
Tính
Đáp án B.