Google
Câu hỏi: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $2a$, $SA$ vuông góc với mặt phẳng đáy và $SA=2a$. Góc giữa đường thẳng $SD$ và mặt phẳng $\left( SAC \right)$ bằng
A. $60{}^\circ $.
B. $30{}^\circ $.
C. $45{}^\circ $.
D. $90{}^\circ $.
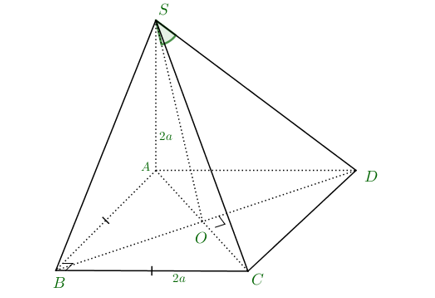Gọi $O$ là giao điểm của $AC$ và $BD$. Ta có $\left\{ \begin{aligned}
& DO\bot AC \\
& DO\bot SA \\
\end{aligned} \right.\Rightarrow DO\bot \left( SAC \right)$
Suy ra góc giữa $SD$ và mặt phẳng $\left( SAC \right)$ là góc $\widehat{OSD}$
Mặt khác $DO=\dfrac{DB}{2}=a\sqrt{2}$, $SD=\sqrt{S{{A}^{2}}+A{{D}^{2}}}=2a\sqrt{2}$
Suy ra $\sin \widehat{OSD}=\dfrac{OD}{SD}=\dfrac{1}{2}$. Vậy góc giữa $SD$ và mặt phẳng $\left( SAC \right)$ là $30{}^\circ $.
A. $60{}^\circ $.
B. $30{}^\circ $.
C. $45{}^\circ $.
D. $90{}^\circ $.
& DO\bot AC \\
& DO\bot SA \\
\end{aligned} \right.\Rightarrow DO\bot \left( SAC \right)$
Suy ra góc giữa $SD$ và mặt phẳng $\left( SAC \right)$ là góc $\widehat{OSD}$
Mặt khác $DO=\dfrac{DB}{2}=a\sqrt{2}$, $SD=\sqrt{S{{A}^{2}}+A{{D}^{2}}}=2a\sqrt{2}$
Suy ra $\sin \widehat{OSD}=\dfrac{OD}{SD}=\dfrac{1}{2}$. Vậy góc giữa $SD$ và mặt phẳng $\left( SAC \right)$ là $30{}^\circ $.
Đáp án B.