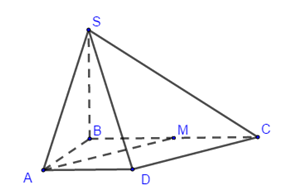
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $B$, $AB=AD=a$, $BC=2a$. Cạnh bên $SB$ vuông góc với đáy và $SB=a\sqrt{7}$...

Vì $M$ là trung điểm của $BC$ nên $MC=MB=\dfrac{BC}{2}=a$ $\Rightarrow AD=MC=a \left( 1 \right)$
Lại có $ABCD$ là hình thang vuông tại $A$ và $B$ nên $AD//BC$ $\Rightarrow AD//MC \left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $ADCM$ là hình bình hành $\Rightarrow AM//DC$
$\Rightarrow d\left( AM,SC \right)=d\left( AM ,\left( SDC \right) \right)=d\left( M,\left( SDC \right) \right)$
Vì $M$ là trung điểm của $BC$ nên $d\left( M,\left( SDC \right) \right)=\dfrac{1}{2}d\left( B,\left( SDC \right) \right)$
Tứ giác $ABMD$ có $\left\{ \begin{aligned}
& AD//BM \\
& AD=BM \\
& \widehat{BAD}={{90}^{\circ }} \\
\end{aligned} \right.$$\Rightarrow ABMD $ là hình vuông $ \Rightarrow BD\bot AM $ và $ AM=a\sqrt{2}$
Vì $AM//DC$ nên có $BD\bot DC$
Mà $DC\bot SB$
Suy ra $CD\bot \left( SBD \right)$ $\Rightarrow \left( SCD \right)\bot \left( SBD \right)$ và chúng có giao tuyến là $SD$
Khi đó có $d\left( B,\left( SCD \right) \right)=d\left( B,SD \right)$
Vì $SB$ vuông góc với đáy nên $SB\bot BD$ $\Rightarrow SBD$ vuông tại $B$
Theo hệ thức lượng trong tam giác vuông có $\dfrac{1}{{{d}^{2}}\left( B,SD \right)}=\dfrac{1}{S{{B}^{2}}}+\dfrac{1}{B{{D}^{2}}}$ $\Rightarrow d\left( B,SD \right)=\sqrt{\dfrac{S{{B}^{2}}.S{{D}^{2}}}{S{{B}^{2}}+S{{D}^{2}}}}=\sqrt{\dfrac{S{{B}^{2}}.A{{M}^{2}}}{S{{B}^{2}}+A{{M}^{2}}}}=\sqrt{\dfrac{7{{a}^{2}}.2{{a}^{2}}}{7{{a}^{2}}+2{{a}^{2}}}}=\dfrac{a\sqrt{14}}{3}$
$\Rightarrow d\left( AM,SC \right)=\dfrac{1}{2}d\left( B,SD \right)=\dfrac{a\sqrt{14}}{6}$.