Câu hỏi: Cho hình chóp
A.
B.
C.
D.
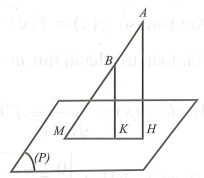
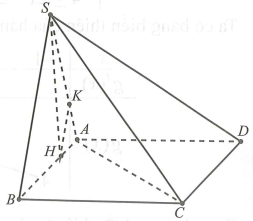
Sử dụng
Sử dụng công thức chuyển điểm: Đường thẳng AB cắt
Xác định khoảng cách
Vì
Lại có
Hay
Ta có:
Kẻ
Nên
Ta có
Xét tam giác
Suy ra
A.
B.
C.
D.
Sử dụng
Sử dụng công thức chuyển điểm: Đường thẳng AB cắt
Xác định khoảng cách
Vì
Lại có
Hay
Ta có:
Kẻ
Nên
Ta có
Xét tam giác
Suy ra
Đáp án B.