Google
Câu hỏi: Cho hình chóp $S.ABC$ có đáy là tam giác đều, tam giác $SAB$ vuông cân tại $S$ và nằm trong mặt phẳng vuông góc với đáy. Biết $SA=\sqrt{6}a$, khoảng cách từ $A$ đến mặt phẳng $\left( SBC \right)$ bằng
A. $\dfrac{6\sqrt{7}a}{7}$.
B. $\dfrac{\sqrt{7}a}{2}$.
C. $\dfrac{3\sqrt{7}a}{7}$.
D. $\sqrt{7}a$.
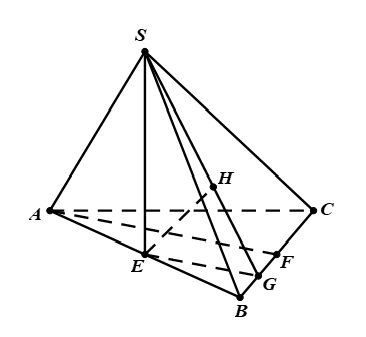Gọi $E$ là trung điểm cạnh $AB$. Khi đó: $SE\bot AB$.
Mà $\left( SAB \right)\bot \left( ABC \right)$. Suy ra: $SE\bot \left( ABC \right)$.
Gọi $F,G$ lần lượt là trung điểm đoạn $BC;BF$.
Tam giác $ABC$ đều nên $AF\bot BC$.
Xét tam giác $ABF$ có $E,G$ lần lượt là trung điểm $AB,BF$ nên $EG//AF$.
Suy ra: $EG\bot BC$.
Ta có: $SE\bot \left( ABC \right)\Rightarrow SE\bot BC$ và $EG\bot BC$.
Suy ra: $BC\bot \left( SEG \right)$ $\Rightarrow \left( SEG \right)\bot \left( SBC \right)$.
Gọi $H$ là hình chiếu vuông góc của $E$ trên $SG$.
Suy ra: $EH\bot \left( SBC \right)$. Nên $d\left( E;\left( SBC \right) \right)=EH$.
Do $\Delta SAB$ vuông cân tại $S; SA=a\sqrt{6}$ nên $AB=SA.\sqrt{2}=2\sqrt{3}a\Rightarrow SE=a\sqrt{3}$.
Tam giác $ABC$ đều cạnh $AB=2\sqrt{3}a$ nên $AF=\dfrac{\sqrt{3}}{2}.2\sqrt{3}a=3a$. Suy ra: $EG=\dfrac{1}{2}AF=\dfrac{3}{2}a$.
Tam giác $SEG$ vuông tại $E$, $EH\bot SG$ nên $EH=\dfrac{ES.EG}{SG}=\dfrac{a\sqrt{3}.\dfrac{3}{2}a}{\sqrt{{{\left( a\sqrt{3} \right)}^{2}}+{{\left( \dfrac{3}{2}a \right)}^{2}}}}=\dfrac{3\sqrt{7}}{7}a$.
Suy ra: $d\left( A;\left( SBC \right) \right)=2.EH=\dfrac{6\sqrt{7}}{7}a$
A. $\dfrac{6\sqrt{7}a}{7}$.
B. $\dfrac{\sqrt{7}a}{2}$.
C. $\dfrac{3\sqrt{7}a}{7}$.
D. $\sqrt{7}a$.
Mà $\left( SAB \right)\bot \left( ABC \right)$. Suy ra: $SE\bot \left( ABC \right)$.
Gọi $F,G$ lần lượt là trung điểm đoạn $BC;BF$.
Tam giác $ABC$ đều nên $AF\bot BC$.
Xét tam giác $ABF$ có $E,G$ lần lượt là trung điểm $AB,BF$ nên $EG//AF$.
Suy ra: $EG\bot BC$.
Ta có: $SE\bot \left( ABC \right)\Rightarrow SE\bot BC$ và $EG\bot BC$.
Suy ra: $BC\bot \left( SEG \right)$ $\Rightarrow \left( SEG \right)\bot \left( SBC \right)$.
Gọi $H$ là hình chiếu vuông góc của $E$ trên $SG$.
Suy ra: $EH\bot \left( SBC \right)$. Nên $d\left( E;\left( SBC \right) \right)=EH$.
Do $\Delta SAB$ vuông cân tại $S; SA=a\sqrt{6}$ nên $AB=SA.\sqrt{2}=2\sqrt{3}a\Rightarrow SE=a\sqrt{3}$.
Tam giác $ABC$ đều cạnh $AB=2\sqrt{3}a$ nên $AF=\dfrac{\sqrt{3}}{2}.2\sqrt{3}a=3a$. Suy ra: $EG=\dfrac{1}{2}AF=\dfrac{3}{2}a$.
Tam giác $SEG$ vuông tại $E$, $EH\bot SG$ nên $EH=\dfrac{ES.EG}{SG}=\dfrac{a\sqrt{3}.\dfrac{3}{2}a}{\sqrt{{{\left( a\sqrt{3} \right)}^{2}}+{{\left( \dfrac{3}{2}a \right)}^{2}}}}=\dfrac{3\sqrt{7}}{7}a$.
Suy ra: $d\left( A;\left( SBC \right) \right)=2.EH=\dfrac{6\sqrt{7}}{7}a$
Đáp án A.