Google
Câu hỏi: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B,$ $BC=a\sqrt{3},$ $AC=2a$. Cạnh bên $SA$ vuông góc với mặt phẳng đáy và $SA=a\sqrt{3}$. Góc giữa đường thẳng $SB$ và mặt phẳng đáy bằng
A. $45{}^\circ $.
B. $90{}^\circ $.
C. $60{}^\circ $.
D. $30{}^\circ $.
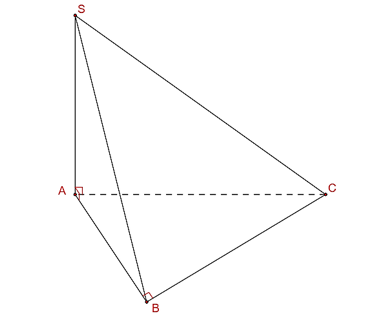Góc giữa đường thẳng $SB$ và mặt phẳng đáy là góc giữa $SB$ và $AB$ hay chính là góc $\widehat{SBA}$, $\tan \widehat{SBA}=\dfrac{SA}{AB}=\dfrac{SA}{\sqrt{A{{C}^{2}}-B{{C}^{2}}}}=\sqrt{3}\Rightarrow \widehat{SBA}=60{}^\circ $.
A. $45{}^\circ $.
B. $90{}^\circ $.
C. $60{}^\circ $.
D. $30{}^\circ $.
Đáp án C.