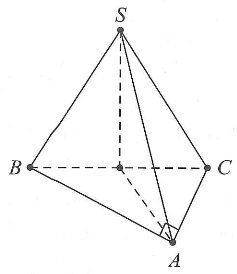
Câu hỏi: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. $AB=a,AC=a\sqrt{3}$. Tam giác SBC đều và nằm trong mặt phẳng vuông với đáy (tham khảo hình vẽ bên). Tính khoảng cách từ điểm B đến mặt phẳng (SAC).
A. $\dfrac{\sqrt{39}a}{13}$
B. $\dfrac{\sqrt{6}a}{2}$
C. $\dfrac{\sqrt{3}a}{2}$
D. $\dfrac{2\sqrt{39}a}{13}$

Gọi H là trung điểm BC
$\Rightarrow SH\bot BC\Rightarrow SH\bot (ABC)$
Gọi K là trung điểm AC suy ra $HK\bot AC$
Kẻ $HE\bot SK(E\in SK)$. Khi đó
$d\left[ B;(SAC) \right]=2.d\left[ H;(SAC) \right]=2.HE$
Lại có $HE=\dfrac{SH.HK}{\sqrt{S{{H}^{2}}+H{{K}^{2}}}}=\dfrac{\sqrt{39}a}{13}$
Vậy khoảng cách cần tính là $2.HE=\dfrac{2\sqrt{39}a}{13}$

A. $\dfrac{\sqrt{39}a}{13}$
B. $\dfrac{\sqrt{6}a}{2}$
C. $\dfrac{\sqrt{3}a}{2}$
D. $\dfrac{2\sqrt{39}a}{13}$
Gọi H là trung điểm BC
$\Rightarrow SH\bot BC\Rightarrow SH\bot (ABC)$
Gọi K là trung điểm AC suy ra $HK\bot AC$
Kẻ $HE\bot SK(E\in SK)$. Khi đó
$d\left[ B;(SAC) \right]=2.d\left[ H;(SAC) \right]=2.HE$
Lại có $HE=\dfrac{SH.HK}{\sqrt{S{{H}^{2}}+H{{K}^{2}}}}=\dfrac{\sqrt{39}a}{13}$
Vậy khoảng cách cần tính là $2.HE=\dfrac{2\sqrt{39}a}{13}$
Đáp án D.