Google
Câu hỏi: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại A, $AB=a$, SA vuông góc với mặt phẳng đáy và $SA=2a$. Gọi $M$ là trung điểm của $BC$. Khoảng cách giữa hai đường thẳng $AC$ và $SM$ bằng
A. $\dfrac{a}{2}$.
B. $\dfrac{a\sqrt{2}}{2}$.
C. $\dfrac{2\sqrt{17}}{17}a$.
D. $\dfrac{2a}{3}$.
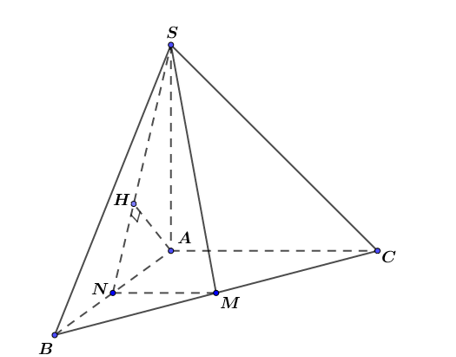Gọi N là trung điểm của AB $\Rightarrow AN=\dfrac{a}{2} \text{v }\grave{\mathrm{a}} MN // AC $.Mặt khác $AC\bot AB \Rightarrow MN \bot AB$.
Gọi H là hình chiếu vuông góc của A lên cạnh $SN \Rightarrow AH\bot SN \left( 1 \right)$.
Ta có $MN\bot AN,MN\bot SA\Rightarrow MN \bot AH \left( 2 \right)$. Từ (1) và (2) suy ra
$AH\bot (SMN)\Rightarrow d\left( A, \left( SMN \right) \right)= AH$
Khi đó:
$ d\left( AC,SM \right)=d\left( AC,\left( SMN \right) \right)=d\left( A,\left( SMN \right) \right)= AH=\dfrac{SA.AN}{\sqrt{S{{A}^{2}}+A{{N}^{2}}}}=\dfrac{2a.\dfrac{a}{2}}{\sqrt{4{{a}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}}}}=\dfrac{2a\sqrt{17}}{17}$.
A. $\dfrac{a}{2}$.
B. $\dfrac{a\sqrt{2}}{2}$.
C. $\dfrac{2\sqrt{17}}{17}a$.
D. $\dfrac{2a}{3}$.
Gọi H là hình chiếu vuông góc của A lên cạnh $SN \Rightarrow AH\bot SN \left( 1 \right)$.
Ta có $MN\bot AN,MN\bot SA\Rightarrow MN \bot AH \left( 2 \right)$. Từ (1) và (2) suy ra
$AH\bot (SMN)\Rightarrow d\left( A, \left( SMN \right) \right)= AH$
Khi đó:
$ d\left( AC,SM \right)=d\left( AC,\left( SMN \right) \right)=d\left( A,\left( SMN \right) \right)= AH=\dfrac{SA.AN}{\sqrt{S{{A}^{2}}+A{{N}^{2}}}}=\dfrac{2a.\dfrac{a}{2}}{\sqrt{4{{a}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}}}}=\dfrac{2a\sqrt{17}}{17}$.
Đáp án C.