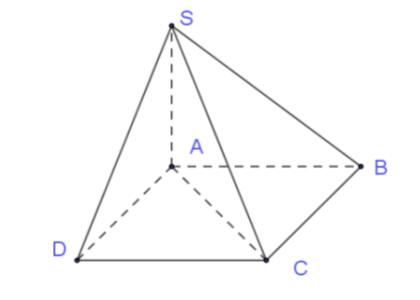
Câu hỏi: Cho hình chóp $S . A B C D$ có đáy là hình thoi cạnh $a$, góc $A B C$ bằng $60^{\circ}$. $S A$ vuông góc với mặt phẳng $(A B C D), S A=\dfrac{a \sqrt{3}}{3}$ (minh họa như hình bên). Góc giữa đường thẳng $S C$ và mặt phẳng $(A B C D)$ bằng
A. $90^{\circ}$.
B. $30^{\circ}$.
C. $45^{\circ}$.
D. $60^{\circ}$.
A. $90^{\circ}$.
B. $30^{\circ}$.
C. $45^{\circ}$.
D. $60^{\circ}$.
Ta có: $S C \cap(A B C D)=C ; S A \perp(A B C D)$ tại $A$.
$\Rightarrow$ Hình chiếu vuông góc của $S C$ lên mặt phẳng $(A B C D)$ là $A C$.
$\Rightarrow$ Góc giữa đường thẳng $S C$ và mặt phẳng $(A B C D)$ là $\alpha=S \widehat{C A}$.
Do $A B C D$ là hình thoi cạnh $a$ và $\widehat{A B C}=60^{\circ}$ nên tam giác $A B C$ đều cạnh $a$. Do đó $A C=a$.
Suy ra: $\tan \widehat{S C A}=\dfrac{S A}{A C}=\dfrac{\sqrt{3}}{3}$. Do đó: $\alpha=\widehat{S B A}=30^{\circ}$.
Vậy góc giữa đường thẳng $S C$ và mặt phẳng $(A B C D)$ bằng $30^{\circ}$.
$\Rightarrow$ Hình chiếu vuông góc của $S C$ lên mặt phẳng $(A B C D)$ là $A C$.
$\Rightarrow$ Góc giữa đường thẳng $S C$ và mặt phẳng $(A B C D)$ là $\alpha=S \widehat{C A}$.
Do $A B C D$ là hình thoi cạnh $a$ và $\widehat{A B C}=60^{\circ}$ nên tam giác $A B C$ đều cạnh $a$. Do đó $A C=a$.
Suy ra: $\tan \widehat{S C A}=\dfrac{S A}{A C}=\dfrac{\sqrt{3}}{3}$. Do đó: $\alpha=\widehat{S B A}=30^{\circ}$.
Vậy góc giữa đường thẳng $S C$ và mặt phẳng $(A B C D)$ bằng $30^{\circ}$.
Đáp án B.