Google
Câu hỏi: Cho hình chóp đều S.ABCD có $SA=a\sqrt{5},AB=a$. Gọi M, N, P, Q lần lượt là trung điểm của SA, SB, SC, SD. Tính cosin của góc giữa hai đường thẳng DN và mặt phẳng $\left( MQP \right)$ ?
A. $\dfrac{\sqrt{2}}{2}.$
B. $\dfrac{1}{2}.$
C. $\dfrac{\sqrt{3}}{2}.$
D. $\dfrac{\sqrt{15}}{6}.$
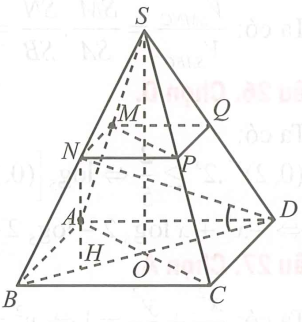
Dễ dàng chứng minh được MNPQ đồng phẳng và $\left( MNPQ \right)//\left( ABCD \right)$ dựa vào tính chất đường trung bình của tam giác.
$\Rightarrow \widehat{\left( DN,\left( MQP \right) \right)}=\widehat{\left( DN,\left( MNP \right) \right)}=\widehat{\left( DN,\left( ABCD \right) \right)}$.
Gọi $O=AC\cap BD\Rightarrow SO\bot \left( ABCD \right)$.
Gọi H là trung điểm của OB.
Xét tam giác SOB có NH là đường trung bình
$\Rightarrow NH//SO\Rightarrow NH\bot \left( ABCD \right)$.
$\Rightarrow DH$ là hình chiếu của DN trên $\left( ABCD \right)$.
$\Rightarrow \widehat{\left( DN,\left( ABCD \right) \right)}=\widehat{\left( DN,DH \right)}=\widehat{NDH}$.
ABCD là hình vuông cạnh $a\Rightarrow BD=a\sqrt{2}\Rightarrow DH=\dfrac{3}{4}BD=\dfrac{3a\sqrt{2}}{4},\ OB=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}.$
Xét tam giác vuông SOB có $SO=\sqrt{S{{B}^{2}}-O{{B}^{2}}}=\dfrac{3a}{\sqrt{2}}\Rightarrow NH=\dfrac{1}{2}SO=\dfrac{3a}{2\sqrt{2}}.$
Xét tam giác vuông NHD có: $ND=\sqrt{N{{H}^{2}}+H{{D}^{2}}}=\sqrt{\dfrac{9{{a}^{2}}}{8}+\dfrac{9{{a}^{2}}}{8}}=\dfrac{3a}{2}.$
$\Rightarrow \cos \widehat{NDH}=\dfrac{DH}{ND}=\dfrac{\dfrac{3a\sqrt{2}}{4}}{\dfrac{3a}{2}}=\dfrac{\sqrt{2}}{2}.$
Lưu ý: Góc giữa đường thẳng và mặt phẳng cắt nhau là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
A. $\dfrac{\sqrt{2}}{2}.$
B. $\dfrac{1}{2}.$
C. $\dfrac{\sqrt{3}}{2}.$
D. $\dfrac{\sqrt{15}}{6}.$
Dễ dàng chứng minh được MNPQ đồng phẳng và $\left( MNPQ \right)//\left( ABCD \right)$ dựa vào tính chất đường trung bình của tam giác.
$\Rightarrow \widehat{\left( DN,\left( MQP \right) \right)}=\widehat{\left( DN,\left( MNP \right) \right)}=\widehat{\left( DN,\left( ABCD \right) \right)}$.
Gọi $O=AC\cap BD\Rightarrow SO\bot \left( ABCD \right)$.
Gọi H là trung điểm của OB.
Xét tam giác SOB có NH là đường trung bình
$\Rightarrow NH//SO\Rightarrow NH\bot \left( ABCD \right)$.
$\Rightarrow DH$ là hình chiếu của DN trên $\left( ABCD \right)$.
$\Rightarrow \widehat{\left( DN,\left( ABCD \right) \right)}=\widehat{\left( DN,DH \right)}=\widehat{NDH}$.
ABCD là hình vuông cạnh $a\Rightarrow BD=a\sqrt{2}\Rightarrow DH=\dfrac{3}{4}BD=\dfrac{3a\sqrt{2}}{4},\ OB=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}.$
Xét tam giác vuông SOB có $SO=\sqrt{S{{B}^{2}}-O{{B}^{2}}}=\dfrac{3a}{\sqrt{2}}\Rightarrow NH=\dfrac{1}{2}SO=\dfrac{3a}{2\sqrt{2}}.$
Xét tam giác vuông NHD có: $ND=\sqrt{N{{H}^{2}}+H{{D}^{2}}}=\sqrt{\dfrac{9{{a}^{2}}}{8}+\dfrac{9{{a}^{2}}}{8}}=\dfrac{3a}{2}.$
$\Rightarrow \cos \widehat{NDH}=\dfrac{DH}{ND}=\dfrac{\dfrac{3a\sqrt{2}}{4}}{\dfrac{3a}{2}}=\dfrac{\sqrt{2}}{2}.$
Lưu ý: Góc giữa đường thẳng và mặt phẳng cắt nhau là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Đáp án A.