Câu hỏi: Cho hình chóp đều
A.
B.
C.
D.
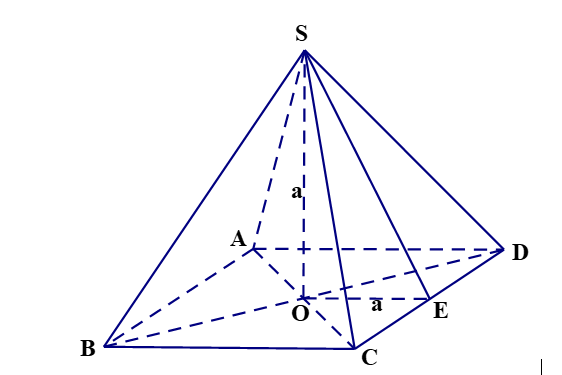
Gọi
Gọi
Dễ thấy tam giác
Suy ra
Vậy
A.
B.
C.
D.
Gọi
Gọi
Dễ thấy tam giác
Suy ra
Vậy
Đáp án B.