Google
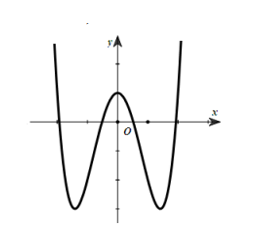
Câu hỏi: Cho hàm số $y=\text{a}{{\text{x}}^{4}}+b{{x}^{2}}+c, (a,b,c\in \mathbb{R})$ có đồ thị là đường cong như hình vẽ dưới đây.
Mệnh đề nào sau đây đúng?
A. $a>0,b>0,c<0$.
B. $a>0,b<0,c>0$.
C. $a>0,b<0,c<0$.
D. $a<0,b>0,c>0$.
A. $a>0,b>0,c<0$.
B. $a>0,b<0,c>0$.
C. $a>0,b<0,c<0$.
D. $a<0,b>0,c>0$.
Do đồ thị hàm số cắt trục $Oy$ tại điểm có tọa độ $\left( 0;c \right)$ nằm phía trên trục $Ox$ nên $c>0$.
Vì $\underset{x\to +\infty }{\mathop{\lim }} y=+\infty $ và $\underset{x\to -\infty }{\mathop{\lim }} y=+\infty $ nên $a>0$.
Hàm số có ba điểm cực trị nên $ab<0\Rightarrow b<0$.
Vì $\underset{x\to +\infty }{\mathop{\lim }} y=+\infty $ và $\underset{x\to -\infty }{\mathop{\lim }} y=+\infty $ nên $a>0$.
Hàm số có ba điểm cực trị nên $ab<0\Rightarrow b<0$.
Đáp án B.