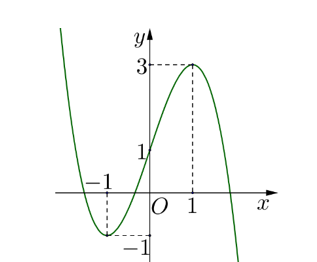
Câu hỏi: Cho hàm số $y=f(x)$ liên tục trên $R$ và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f\left( f(\cos x) \right)=m$ có nghiệm thuộc khoảng $\left( \dfrac{\pi }{2};\dfrac{3\pi }{2} \right)?$
A. $5.$
B. $3.$
C. $4.$
D. $2.$
A. $5.$
B. $3.$
C. $4.$
D. $2.$
Đặt $t=\cos x$, vì $x\in \left( \dfrac{\pi }{2}; \dfrac{3\pi }{2} \right)\to t\in \left[ -1; 0 \right)$ $\to f\left( t \right)\in \left[ -1; 1 \right)$
Điều kiện bài toán $\Leftrightarrow pt f\left( f\left( t \right) \right)=m$ có nghiệm $t\in \left[ -1; 0 \right)$ $\Rightarrow -1\le m<3$
Kết hợp với điều kiện $m\in \mathbb{Z}$ $\Rightarrow m=\left\{ -1; 0; 1; 2 \right\}$.
Điều kiện bài toán $\Leftrightarrow pt f\left( f\left( t \right) \right)=m$ có nghiệm $t\in \left[ -1; 0 \right)$ $\Rightarrow -1\le m<3$
Kết hợp với điều kiện $m\in \mathbb{Z}$ $\Rightarrow m=\left\{ -1; 0; 1; 2 \right\}$.
Đáp án C.