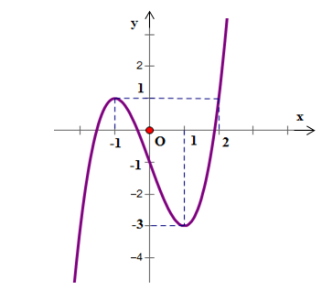
Cho hàm số $y=f(x)$ có đồ thị hình bên dưới. Phương trình $f\left[ f(\cos x)-1 \right]=0$ có bao nhiêu nghiệm thuộc đoạn $\left[ 0;2\pi \right]$ ?

Xét hàm số $t=\cos x;x\in \left[ 0;2\pi \right]\Rightarrow t\in \left[ -1;1 \right]$.
Ta có ${t}'(x)=-\sin x\text{;}\ {t}'(x)\text{=0}\Leftrightarrow \left[ \begin{aligned}
& x=0 \\
& x=\pi \\
& x=2\pi \\
\end{aligned} \right.$
Lập bảng biến thiên của hàm số $t=\cos x$ ta có :

Với $t=-1$ thì phương trình $\cos x=t$ có duy nhất một nghiệm trên $\left[ 0;2\pi \right]$
Với $t\in (-1;1\!\!]\!\!$ thì phương trình $\cos x=t$ có hai nghiệm phân biệt trên $\left[ 0;2\pi \right]$.
Ta có
$f\left[ f(t)-1 \right]=0\Rightarrow \left[ \begin{aligned}
& f(t)-1=a \\
& f(t)-1=b \\
& f(t)-1=c \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& f(t)=a+1;1<a<2 \\
& f(t)=b+1;-1<b<0 \\
& f(t)=c+1;-2<c<-1 \\
\end{aligned} \right.$
Vẽ các đường thẳng $y=a+1;y=b+1;y=c+1$ trên trục tọa độ ta có

TH1: $f(t)=a+1$. Khi đó $2<a+1<3$ phương trình $f(t)=a+1$ có nghiệm $t>2$ suy ra phương trình $f\left( \cos x \right)=a+1$ vô nghiệm).
TH2: $f(t)=b+1$. Khi đó: $0<b+1<1$ phương trình $f(t)=b+1$ có 3 nghiệm trong đó chỉ có $1$ nghiệm $t\in (-1;0)$ thỏa mãn suy ra phương trình $f\left[ f(\cos x)-1 \right]=0$ có hai nghiệm phân biệt thuộc $\left[ 0;2\pi \right]$.
TH3: $f(t)=c+1$ Khi đó $-1<c+1<0$ phương trình $f(t)=c+1$ có 3 nghiệm trong đó chỉ có $1$ nghiệm $t\in (-1;0)$ thỏa mãn suy ra phương trình $f\left[ f(\cos x)-1 \right]=0$ có hai nghiệm phân biệt thuộc $\left[ 0;2\pi \right]$.
Vậy phương trình $f\left[ f(\cos x\text{) - 1} \right]=0$ có $4$ nghiệm thuộc đoạn $\left[ 0;2\pi \right]$.