Google
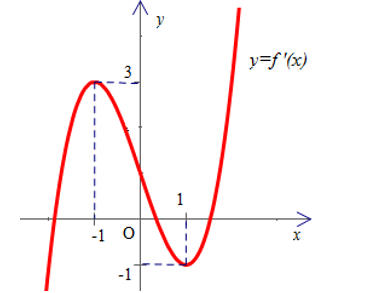
Câu hỏi: Cho hàm số $y=f(x)$ có đồ thị của hàm số $f^{\prime}(x)$ như sau:
Trên khoảng $(-10 ; 10)$ có tất cả bao nhiêu số nguyên của $m$ để hàm số $g(x)=f(x)+m x+$ 2020 có đúng một cực trị?
A. 15 .
B. 0 .
C. 13 .
D. 14 .
A. 15 .
B. 0 .
C. 13 .
D. 14 .
Ta có: $g^{\prime}(x)=f^{\prime}(x)+m$.
$g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x)+m=0 \Leftrightarrow f^{\prime}(x)=-m$. (1)
Hàm số $g(x)$ có đúng một cực trị khi (1) có nghiệm duy nhất hay đồ thị hàm số $y=f^{\prime}(x)$ cắt đường thẳng $y=-m$ tại duy nhất một điểm.
Dựa vào đồ thị hàm số $y=f^{\prime}(x)$ ta có kết quả: $\left[\begin{array}{l}-m>3 \\ -m<-1\end{array} \Leftrightarrow\left[\begin{array}{l}m<-3 \\ m>1\end{array}\right.\right.$
Do $m \in \mathbb{Z}$ và $m \in(-10 ; 10) \Rightarrow m=-9 ;-8 ; \ldots ;-4 ; 2 ; 3 ; \ldots ; 8 ; 9 \Rightarrow$ có 14 giá trị của $m$ thỏa mãn.
$g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x)+m=0 \Leftrightarrow f^{\prime}(x)=-m$. (1)
Hàm số $g(x)$ có đúng một cực trị khi (1) có nghiệm duy nhất hay đồ thị hàm số $y=f^{\prime}(x)$ cắt đường thẳng $y=-m$ tại duy nhất một điểm.
Dựa vào đồ thị hàm số $y=f^{\prime}(x)$ ta có kết quả: $\left[\begin{array}{l}-m>3 \\ -m<-1\end{array} \Leftrightarrow\left[\begin{array}{l}m<-3 \\ m>1\end{array}\right.\right.$
Do $m \in \mathbb{Z}$ và $m \in(-10 ; 10) \Rightarrow m=-9 ;-8 ; \ldots ;-4 ; 2 ; 3 ; \ldots ; 8 ; 9 \Rightarrow$ có 14 giá trị của $m$ thỏa mãn.
Đáp án D.