Google
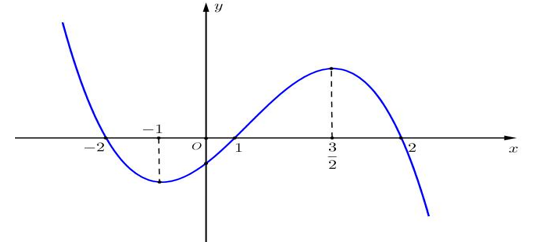
Câu hỏi: Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$, thỏa mãn $f(2) \leq f(-2)=2020$. Hàm số $y={f}'(x)$ có đồ thị như hình vẽ.
Hàm số $g(x)=[2020-f(x)]^2$ nghịch biến trên khoảng
A. $(0 ; 2)$.
B. $(-2 ;-1)$.
C. $(1 ; 2)$.
D. $(-2 ; 2)$.
A. $(0 ; 2)$.
B. $(-2 ;-1)$.
C. $(1 ; 2)$.
D. $(-2 ; 2)$.
Từ đồ thị hàm số $y={f}'(x)$ ta có bảng biến thiên của hàm số $y=f(x)$
$g(x)={{[2020-f(x)]}^{2}}\Rightarrow {g}'(x)=-2{f}'\left( x \right).[2020-f(x)]$.
Do $f\left( x \right)\le f(-2)=2020\Rightarrow 2020-f\left( x \right)\ge 0\Rightarrow {g}'\left( x \right)<0\Rightarrow {f}'\left( x \right)>0\Leftrightarrow \left[ \begin{aligned}
& x<-2 \\
& 1<x<2 \\
\end{aligned} \right..$
Vậy hàm số $g(x)=[2020-f(x)]^2$ nghịch biến trên khoảng $\left( -\infty ;-2 \right)$ và $\left( 1;2 \right)$.
Do $f\left( x \right)\le f(-2)=2020\Rightarrow 2020-f\left( x \right)\ge 0\Rightarrow {g}'\left( x \right)<0\Rightarrow {f}'\left( x \right)>0\Leftrightarrow \left[ \begin{aligned}
& x<-2 \\
& 1<x<2 \\
\end{aligned} \right..$
Vậy hàm số $g(x)=[2020-f(x)]^2$ nghịch biến trên khoảng $\left( -\infty ;-2 \right)$ và $\left( 1;2 \right)$.
Đáp án C.