Câu hỏi: Cho hàm số
Có bao nhiêu số nguyên
A. 2017.
B. 2020.
C. 2019.
D. 2018.
Xét hàm số
Ta có
Ta có bảng xét dấu theo khoảng như sau
(với
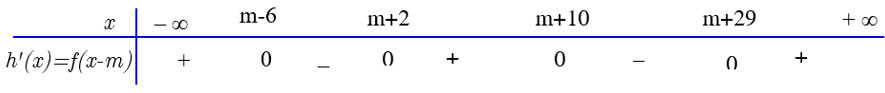
Để hàm số đồng biến trên
Suy ra
Có bao nhiêu số nguyên
A. 2017.
B. 2020.
C. 2019.
D. 2018.
Xét hàm số
Ta có
Ta có bảng xét dấu theo khoảng như sau
(với
Để hàm số đồng biến trên
Suy ra
Đáp án D.
