Google
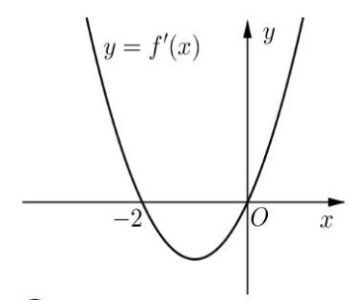
Câu hỏi: Cho hàm số $y=f\left( x \right)$ xác định và liên tục trên $\mathbb{R}$ có đồ thị hàm số ${f}'\left( x \right)$ như hình vẽ. Hàm số $y=f\left( x+2 \right)$ nghịch biến trên khoảng nào sau đây?
A. $\left( -\infty ;-4 \right).$
B. $\left( -2;0 \right).$
C. $\left( -4;-2 \right).$
D. $\left( -2;+\infty \right).$
B. $\left( -2;0 \right).$
C. $\left( -4;-2 \right).$
D. $\left( -2;+\infty \right).$
Ta có bảng xét dấu ${f}'\left( x \right)>0 \forall x\in \left( -\infty ; -2 \right)\cup \left( 0 ; +\infty \right)$ ; ${f}'\left( x \right)<0 \forall x\in \left( -2 ; 0 \right)$
Ta có: $y=f\left( x+2 \right)\Rightarrow y'=f'\left( x+2 \right)$
Hàm số $y=f\left( x+2 \right)$ nghịch biến $\Leftrightarrow $ ${f}'\left( x+2 \right)<0\Leftrightarrow -2<x+2<0\Leftrightarrow -4<x<-2$
Vậy hàm số $y=f\left( x+2 \right)$ nghịch biến trên khoảng $\left( -4;-2 \right).$
Ta có: $y=f\left( x+2 \right)\Rightarrow y'=f'\left( x+2 \right)$
Hàm số $y=f\left( x+2 \right)$ nghịch biến $\Leftrightarrow $ ${f}'\left( x+2 \right)<0\Leftrightarrow -2<x+2<0\Leftrightarrow -4<x<-2$
Vậy hàm số $y=f\left( x+2 \right)$ nghịch biến trên khoảng $\left( -4;-2 \right).$
Đáp án C.