Google
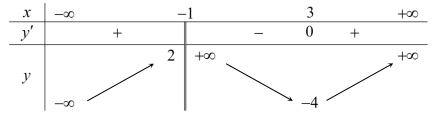
Câu hỏi: Cho hàm số $y=f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ -1 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình sau:
Tìm tập hợp tất cả các giá trị của tham số thực $m$ sao cho phương trình $f\left( x \right)=m$ có đúng ba nghiệm thực phân biệt.
A. $\left( -4;2 \right]$.
B. $\left( -4;2 \right)$.
C. $\left[ -4;2 \right)$.
D. $\left( -\infty ;2 \right]$.
A. $\left( -4;2 \right]$.
B. $\left( -4;2 \right)$.
C. $\left[ -4;2 \right)$.
D. $\left( -\infty ;2 \right]$.
Số nghiệm của phương trình $f\left( x \right)=m$ bằng số giao điểm của hai đồ thị hàm số $y=f\left( x \right)$ và $y=m$. Dựa vào bảng biến thiên ta thấy để phương trình đã cho có đúng ba nghiệm thực phân biệt thì $m\in \left( -4;2 \right)$Đáp án B.