Google
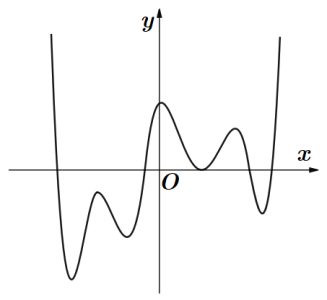
Câu hỏi: Cho hàm số $y=f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ (chỉ cắt trục hoành tại $5$ điểm phân biệt và có $7$ điểm cực trị).
Biết đồ thị của ${f}'\left( x \right)$ không tiếp xúc với trục hoành. Phương trình $f\left( x \right){{2023}^{{f}'\left( x \right)}}+{f}'\left( x \right){{2024}^{f\left( x \right)}}=f\left( x \right)+{f}'\left( x \right)$ có ít nhất bao nhiêu nghiệm thực phân biệt.
A. $11$.
B. $12$.
C. $10$.
D. $13$.
A. $11$.
B. $12$.
C. $10$.
D. $13$.
Ta có $f\left( x \right){{2023}^{{f}'\left( x \right)}}+{f}'\left( x \right){{2024}^{f\left( x \right)}}=f\left( x \right)+{f}'\left( x \right)$
$\Leftrightarrow f\left( x \right)\left( {{2023}^{{f}'\left( x \right)}}-1 \right)+{f}'\left( x \right)\left( {{2024}^{f\left( x \right)}}-1 \right)=0$.
Dễ thấy nghiệm của phương trình ${f}'\left( x \right)=0$ hoặc $f\left( x \right)=0$ thỏa phương trình ban đầu.
Từ đồ thị hàm số $f\left( x \right)$ ta thấy được phương trình $f\left( x \right)=0$ có $5$ nghiệm phân biệt, phương trình ${f}'\left( x \right)=0$ có $7$ nghiệm phân biệt. Do $f\left( x \right)=0$ có một nghiệm bội chẵn nên tổng số nghiệm thực phân biệt của phương trình $f\left( x \right)=0$ và ${f}'\left( x \right)=0$ là $11$.
Nên phương trình $f\left( x \right){{2023}^{{f}'\left( x \right)}}+{f}'\left( x \right){{2024}^{f\left( x \right)}}=f\left( x \right)+{f}'\left( x \right)$ có ít nhất $11$ nghiệm.
$\Leftrightarrow f\left( x \right)\left( {{2023}^{{f}'\left( x \right)}}-1 \right)+{f}'\left( x \right)\left( {{2024}^{f\left( x \right)}}-1 \right)=0$.
Dễ thấy nghiệm của phương trình ${f}'\left( x \right)=0$ hoặc $f\left( x \right)=0$ thỏa phương trình ban đầu.
Từ đồ thị hàm số $f\left( x \right)$ ta thấy được phương trình $f\left( x \right)=0$ có $5$ nghiệm phân biệt, phương trình ${f}'\left( x \right)=0$ có $7$ nghiệm phân biệt. Do $f\left( x \right)=0$ có một nghiệm bội chẵn nên tổng số nghiệm thực phân biệt của phương trình $f\left( x \right)=0$ và ${f}'\left( x \right)=0$ là $11$.
Nên phương trình $f\left( x \right){{2023}^{{f}'\left( x \right)}}+{f}'\left( x \right){{2024}^{f\left( x \right)}}=f\left( x \right)+{f}'\left( x \right)$ có ít nhất $11$ nghiệm.
Đáp án A.