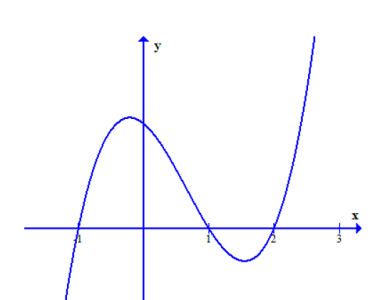
Câu hỏi: Cho hàm số $y=f\left( x \right)$ liên tục và xác định trên $R$ có đồ thị đạo hàm $f'\left( x \right)$ được cho như hình vẽ. Hàm số $y=f\left( {{x}^{2}}-1 \right)$ đồng biến trên khoảng nào sau đây?
A. $\left( 1;+\infty \right)$.
B. $\left( -\infty ;-1 \right)$.
C. $\left( 0;1 \right)$.
D. $\left( 1;2 \right)$.
A. $\left( 1;+\infty \right)$.
B. $\left( -\infty ;-1 \right)$.
C. $\left( 0;1 \right)$.
D. $\left( 1;2 \right)$.
$y=f\left( {{x}^{2}}-1 \right)\Rightarrow y'=2x.f'\left( {{x}^{2}}-1 \right)$.
$2x=0\Leftrightarrow x=0$.
$f'\left( {{x}^{2}}-1 \right)>0\Leftrightarrow \left[ \begin{aligned}
& -1<{{x}^{2}}-1<1 \\
& {{x}^{2}}-1>2 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& 0<{{x}^{2}}<2 \\
& {{x}^{2}}>3 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& -\sqrt{2}<x<\sqrt{2} \\
& x<-\sqrt{3}\bigcup x>\sqrt{3} \\
\end{aligned} \right.$.
Bảng biến thiên:

Dựa vào bảng biến thiên: hàm số đồng biến trên khoảng $\left( 0;1 \right)\subset \left( 0;\sqrt{2} \right)$.
$2x=0\Leftrightarrow x=0$.
$f'\left( {{x}^{2}}-1 \right)>0\Leftrightarrow \left[ \begin{aligned}
& -1<{{x}^{2}}-1<1 \\
& {{x}^{2}}-1>2 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& 0<{{x}^{2}}<2 \\
& {{x}^{2}}>3 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& -\sqrt{2}<x<\sqrt{2} \\
& x<-\sqrt{3}\bigcup x>\sqrt{3} \\
\end{aligned} \right.$.
Bảng biến thiên:
Dựa vào bảng biến thiên: hàm số đồng biến trên khoảng $\left( 0;1 \right)\subset \left( 0;\sqrt{2} \right)$.
Đáp án C.