Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có...

Ta có: $f'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=12 \\
& x=0 \\
& x=2 \\
\end{aligned} \right.$. Bảng xét dấu
Do đó hàm số $y=f\left( x \right)$ đạt cực trị tại $x=0$ và $x=2$.
Xét $y=f\left( {{x}^{2}}-2022x+2021m \right)$ có đạo hàm $y'=\left( 2x-2022 \right).f'\left( {{x}^{2}}-2022x+2021m \right)$.
$y'=0\Leftrightarrow \left[ \begin{aligned}
& x=1011 \\
& f'\left( {{x}^{2}}-2022x+2021m \right)=0\Leftrightarrow \left[ \begin{aligned}
& {{x}^{2}}-2022x+2021m=0 \\
& {{x}^{2}}-2022x+2021m=2 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& {{x}^{2}}-2022x=-2021m \\
& {{x}^{2}}-2022x-2=-2021m \\
\end{aligned} \right. \\
\end{aligned} \right. $Xét các hàm số $ g\left( x \right)={{x}^{2}}-2022x $ và $ h\left( x \right)={{x}^{2}}-2022x-2 $, với $ x>0$.
$g'\left( x \right)=2x-2022$ ; $g'\left( x \right)=0\Leftrightarrow x=1011$
Bảng biến thiên:
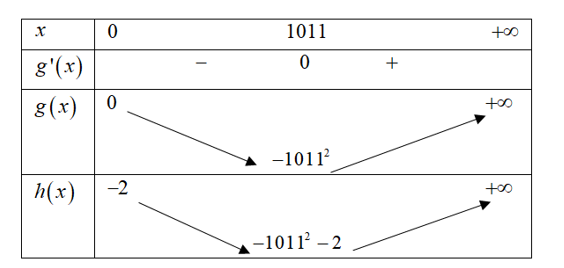Vậy, hàm số có 3 điểm cực trị dương $\Leftrightarrow \left[ \begin{aligned}
& -{{1011}^{2}}-2<-2021m\le -{{1011}^{2}} \\
& -2021m\ge 0 \\
\end{aligned} \right.$
$\Leftrightarrow \left[ \begin{aligned}
& \dfrac{1022121}{2021}\le m<\dfrac{1022123}{2021} \\
& m\le 0 \\
\end{aligned} \right.$.
Kết hợp với giả thiết $\Rightarrow m\in \left\{ -2020;-2019;...;0 \right\}$