Google
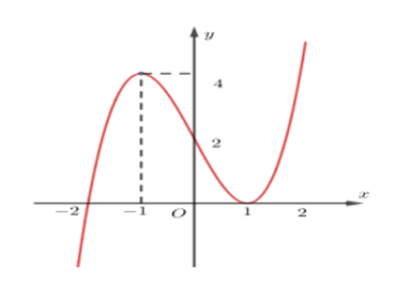
Câu hỏi: Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ.
Có tất cả bao nhiêu giá trị nguyên của tham số $m$ để phương trình $3f\left( {{\left| x \right|}^{3}}-3\left| x \right|+2 \right)-m+1=0$ có $8$ nghiệm phân biệt
A. $6$.
B. $7$.
C. $8$.
D. $5$.
A. $6$.
B. $7$.
C. $8$.
D. $5$.
Xét hàm số $f\left( x \right)=a\left( x+2 \right){{\left( x-1 \right)}^{2}}$. Vì $f\left( 0 \right)=2\Leftrightarrow 2a=2\Leftrightarrow a=1$.
$\Rightarrow f\left( x \right)=\left( x+2 \right){{\left( x-1 \right)}^{2}}={{x}^{3}}-3x+2$.
Phương trình: $3f\left( {{\left| x \right|}^{3}}-3\left| x \right|+2 \right)-m+1=0\Leftrightarrow f\left( {{\left| x \right|}^{3}}-3\left| x \right|+2 \right)=\dfrac{m-1}{3}\left( 1 \right)$.
Sử dụng phương pháp ghép trục :
Phương trình $\left( 1 \right)$ có $8$ nghiệm phân biệt $0<\dfrac{m-1}{3}<2\Leftrightarrow 1<m<7$. Vậy có 5 giá trị nguyên m thoả mãn.
$\Rightarrow f\left( x \right)=\left( x+2 \right){{\left( x-1 \right)}^{2}}={{x}^{3}}-3x+2$.
Phương trình: $3f\left( {{\left| x \right|}^{3}}-3\left| x \right|+2 \right)-m+1=0\Leftrightarrow f\left( {{\left| x \right|}^{3}}-3\left| x \right|+2 \right)=\dfrac{m-1}{3}\left( 1 \right)$.
Sử dụng phương pháp ghép trục :
Phương trình $\left( 1 \right)$ có $8$ nghiệm phân biệt $0<\dfrac{m-1}{3}<2\Leftrightarrow 1<m<7$. Vậy có 5 giá trị nguyên m thoả mãn.
Đáp án D.