Google
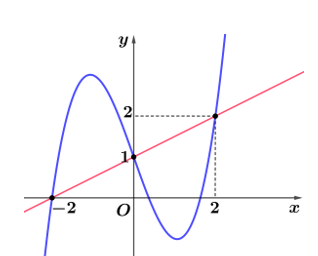
Câu hỏi: Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$. Đồ thị hàm số $y=f'\left( \sqrt[3]{x} \right)$ được cho trong hình bên. Hàm số $g\left( x \right)=\left| f\left( x \right)-\dfrac{1}{8}{{x}^{4}}-x \right|$ có tối đa bao nhiêu điểm cực đại?
A. $2$.
B. $3$.
C. $4$.
D. $5$.
B. $3$.
C. $4$.
D. $5$.
Đặt $h\left( x \right)=f\left( x \right)-\dfrac{1}{8}{{x}^{4}}-x$.
Ta có: $h'\left( x \right)=f'\left( x \right)-\dfrac{1}{2}{{x}^{3}}-1\xrightarrow{h'\left( x \right)=0}f'\left( x \right)=\dfrac{1}{2}{{x}^{3}}+1$.
Đặt $x=\sqrt[3]{t}$. Khi đó phương trình trở thành $f'\left( \sqrt[3]{t} \right)=\dfrac{1}{2}t+1\Leftrightarrow \left[ \begin{aligned}
& t=-2 \\
& t=0 \\
& t=2 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=\sqrt[3]{-2} \\
& x=0 \\
& x=\sqrt[3]{2} \\
\end{aligned} \right.$.
Bảng biến thiên của hàm số $y=h\left( x \right)$ :
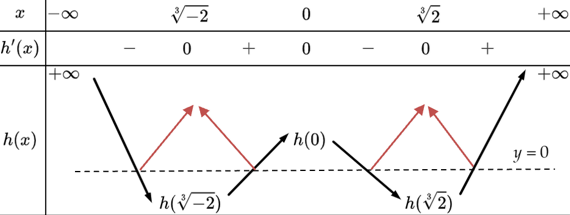Khi đó, hàm số $g\left( x \right)=\left| h\left( x \right) \right|$ có số điểm cực đại nhiều nhất $\Leftrightarrow h\left( x \right)=0$ có 4 nghiệm.
Vậy hàm số $g\left( x \right)=\left| h\left( x \right) \right|$ có tối đa 3 điểm cực đại.
Ta có: $h'\left( x \right)=f'\left( x \right)-\dfrac{1}{2}{{x}^{3}}-1\xrightarrow{h'\left( x \right)=0}f'\left( x \right)=\dfrac{1}{2}{{x}^{3}}+1$.
Đặt $x=\sqrt[3]{t}$. Khi đó phương trình trở thành $f'\left( \sqrt[3]{t} \right)=\dfrac{1}{2}t+1\Leftrightarrow \left[ \begin{aligned}
& t=-2 \\
& t=0 \\
& t=2 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=\sqrt[3]{-2} \\
& x=0 \\
& x=\sqrt[3]{2} \\
\end{aligned} \right.$.
Vậy hàm số $g\left( x \right)=\left| h\left( x \right) \right|$ có tối đa 3 điểm cực đại.
Đáp án B.