Google
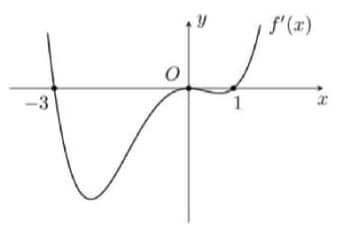
Câu hỏi: Cho hàm số $y=f\left( x \right)$ là hàm đa thức có $f\left( -3 \right)<0$ và đồ thị $f'\left( x \right)$ như hình vẽ bên dưới. số điểm cực đại của hàm số $g\left( x \right)={{\left[ f\left( x-1 \right) \right]}^{1982}}$
A. $3$.
B. $2$.
C. $1$.
D. $4$.
B. $2$.
C. $1$.
D. $4$.
Ta có $g'\left( x \right)=1982.{{\left[ f\left( x-1 \right) \right]}^{1981}}.f'\left( x-1 \right)$
$\Rightarrow g'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& f\left( x-1 \right)=0 \\
& f'\left( x-1 \right)=0\Leftrightarrow \left[ \begin{aligned}
& x-1=-3 \\
& x-1=1 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=-2 \\
& x=2 \\
\end{aligned} \right. \\
\end{aligned} \right.$
Xét bảng biến thiên của $f\left( x \right)$
Dựa vào bảng biển thiên ta thấy $f\left( x-1 \right)=0$ có 1 nghiệm.
Suy ra $g\left( x \right)$ có 3 điểm cực trị, mặt khác $\underset{x\to +\infty }{\mathop{\lim }} g\left( x \right)=+\infty $ nên $g\left( x \right)$ có 1 điểm cực đại.
$\Rightarrow g'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& f\left( x-1 \right)=0 \\
& f'\left( x-1 \right)=0\Leftrightarrow \left[ \begin{aligned}
& x-1=-3 \\
& x-1=1 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=-2 \\
& x=2 \\
\end{aligned} \right. \\
\end{aligned} \right.$
Xét bảng biến thiên của $f\left( x \right)$
Suy ra $g\left( x \right)$ có 3 điểm cực trị, mặt khác $\underset{x\to +\infty }{\mathop{\lim }} g\left( x \right)=+\infty $ nên $g\left( x \right)$ có 1 điểm cực đại.
Đáp án C.